Kezdőlap


Feladat:	2150. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dosztányi Zsuzsa
Füzet:	1987/május, 229 - 230. oldal		PDF \| MathML
Témakör(ök):	Newton-féle gravitációs erő, Síkinga, Feladat
Hivatkozás(ok):	Feladatok: 1986/szeptember: 2150. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az inga lengésideje ( $T = 2 \cdot π \sqrt[]{l / g}$ ) adott $l$ hosszúság esetén csak a nehézségi gyorsulás nagyságától függ. Vizsgáljuk meg, hogyan függ $g$ a bolygó középpontjától mért $r$ távolságtól! Legyen $R$ a bolygó sugara, $M$ a tömege, $ϱ$ pedig a sűrűsége.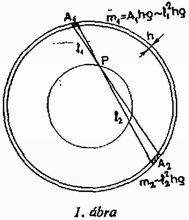
Ha $r ≧ R,$ akkor az $m$ tömegű testre ható erő $F = f \cdot M \cdot m / r^{2},$ vagyis $g = f M / r^{2} .$ Ebből látható, hogy $g$ a magasság növekedésével csökken, vagyis az inga lengésideje nő. Így Andrásnak igaza van.

1. ábra

r < R,

akkor a nehézségi gyorsulás az alábbi gondolatmenettel határozható meg. Osszuk fel a fejünk felett lévő részt vékony gömbhéjakra (1. ábra). Belátjuk, hogy az ábrán vonalkázással jelölt két kis tömegdarab vonzóereje egyenlő nagyságú. Legyen a két darab felülete

A_{1},

illetve

A_{2}

, a

P

ponttól mért távolságuk pedig

l_{1}

és

l_{2}

. Az egyes darabok tömege arányos az

A_{i}

felülettel, ez viszont az

l_{i}

távolság négyzetével arányos. Ebből az következik, hogy a két darab által kifejtett vonzóerő egyenlő, hiszen a tömegvonzási erő fordítottan arányos a távolság négyzetével. Mivel a fenti módon az egész gömbhéj maradék nélkül felosztható anyagdarabka-párokra, a gömbhéj egésze nem fejt ki gravitációs erőt a belsejében levő testekre. Mivel ez az érvelés a "fejünk fölött levő'' valamennyi gömbhéjra érvényes, végül azt kapjuk, hogy

r < R

esetén a nehézségi gyorsulás akkora, mint egy

r

sugarú bolygó felszínén. Ez utóbbi viszont állandó

ϱ

sűrűségnél

\begin{matrix} g = f \cdot \frac{4 \cdot r^{3} \cdot π}{3} \cdot ϱ \cdot \frac{1}{r^{2}} = k \cdot r, \end{matrix}

ahol

k

egy állandó. Tehát

g

a bolygó középpontja felé haladva szintén csökken; Jutkának is igaza van.
A nehézségi gyorsulás nagyságát az

r

távolság függvényében felrajzolva a 2. ábrán látható összefüggést kapjuk.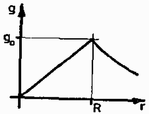

2. ábra