Kezdőlap


Feladat:	2093. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Cynolter Gábor
Füzet:	1987/január, 40 - 45. oldal		PDF \| MathML
Témakör(ök):	Erők forgatónyomatéka, Erőrendszer eredője, Arkhimédész törvénye, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1986/január: 2093. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egyszerűség kedvéért vegyük a súrlódást $0$ -nak a henger felső, száraz pereménél. Írjuk fel az erő és nyomatéki egyensúlyokat az 1. ábra szerinti helyzetben, tehát $α > 45^{\circ}$ esetén.

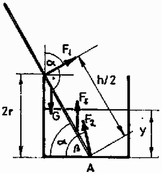1. ábra

\begin{matrix} Σ F_{x} = 0, & F_{1} \cdot sin α = F_{2} \cdot cos β, \\ Σ F_{y} = 0, & G = F_{f} + F_{1} \cdot cos α + F_{2} \cdot sin β, \\ Σ M_{A} = 0, & G \cdot \frac{h}{2} \cdot cos α = F_{1} \cdot \frac{2 r}{sin α} + F_{f} \frac{y / 2}{tgα} . \end{matrix}

Mivel a vékony pálca keresztmetszete nem adott, vezessük be erőegységként a pálca egységnyi hosszának a súlyát!

\begin{matrix} f_{1} = F_{1} / A \cdot ϱ \cdot g, \\ f_{2} = F_{2} / A \cdot ϱ \cdot g . \end{matrix}

Mivel

\begin{matrix} G = h \cdot A \cdot ϱ \cdot g, \end{matrix}

\begin{matrix} F_{f} = \frac{y}{sin α} A \cdot ϱ \cdot r \cdot g, \end{matrix}

ezért

\begin{matrix} f_{1} \cdot sin α = f_{2} \cdot cos β, \end{matrix}

(1)

\begin{matrix} h = \frac{y}{sin α} \cdot \frac{ϱ_{v}}{ϱ} + f_{1} cos α + f_{2} sin β, \end{matrix}

(2)

\begin{matrix} h \cdot \frac{h}{2} cos α = f_{1} \cdot \frac{2 r}{sin α} + \frac{y}{sin α} \cdot \frac{ϱ_{v}}{ϱ} \cdot \frac{y / 2}{tgα} . \end{matrix}

(3)

Mivel az

F_{2}

vízszintes komponense tapadási súrlódási erő:

\begin{matrix} - μ ≦ \frac{F_{2} \cdot cos β}{F_{2} \cdot sin β} ≦ μ, azaz \end{matrix}

\begin{matrix} - μ ≦ ctgβ≦μ. \end{matrix}

Ezen kívül feltétel még, hogy

\begin{matrix} f_{1} ≧ 0; f_{2} ≧ 0. \end{matrix}

Az erő és nyomatéki egyensúlyok a 2. ábra szerinti helyzetben, tehát

α < 45^{\circ}

esetén:

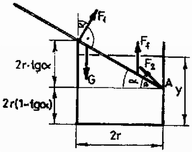2. ábra

\begin{matrix} Σ F_{x} = 0, F_{1} \cdot sin α = F_{2} cos β; \\ Σ F_{y} = 0, G = F_{f} + F_{1} \cdot cos α + F_{2} \cdot sin β; \\ Σ M_{A} = 0, G \cdot \frac{h}{2} \cdot cos α = F_{1} \cdot \frac{2 r}{cos α} + F_{f} \cdot \frac{[y - 2 r (1 - tgα)] / 2}{tgα} . \end{matrix}

A felhajtóerő:

\begin{matrix} F_{f} = 0, ha y - 2 r (1 - tgα) < 0; \\ F_{f} = \frac{y - 2 r (1 - tg α)}{sin α} A \cdot ϱ_{v} g, ha \\ y - 2 r (1 - tg α) = 0. \end{matrix}

Először keressük az egyensúlyi helyzeteket ebben a két esetben. Vigyázat: a

45^{\circ}

-kal való egyenlőséget, azaz a sarokba szorult helyzetet óvatosan kerültük.
Ezért ha

y - 2 r (1 - tg α) < 0

\begin{matrix} f_{1} sin α = f_{2} cos β, \end{matrix}

(1')

\begin{matrix} ϱ_{v} h = \frac{y - 2 r (1 - tg α)}{sin α} \frac{ϱ_{v}}{ϱ} + f_{1} cos α + f_{2} sin β, \end{matrix}

(2')

\begin{matrix} h \cdot \frac{h}{2} \cdot cos α = f_{1} \frac{2 r}{cos α} + \frac{{[y - 2 r (1 - tg α)]}^{2}}{2 sin α \cdot tg α} \frac{ϱ_{v}}{ϱ} . \end{matrix}

(3')

F_{2}

függőleges komponense tapadási súrlódási erő, ezért

\begin{matrix} - μ ≦ \frac{F_{2} \cdot sin β}{F_{2} \cdot cos β} ≦ μ, azaz \end{matrix}

\begin{matrix} - μ ≦ tg β ≦ μ . \end{matrix}

Ugyancsak feltétel az

f_{1} ≧ 0

f_{2} ≧ 0

egyenlőtlenségek teljesülése.
Ezért ha

y - 2 r (1 - tg α) < 0

\begin{matrix} f_{1} sin α = f_{2} cos β, \end{matrix}

(1'')

\begin{matrix} h = f_{1} cos α + f_{2} sin β, \end{matrix}

(2'')

\begin{matrix} \frac{h^{2}}{2} cos α = f_{1} \cdot \frac{2 r}{cos α} . \end{matrix}

(3'')

(1, 2, 3) megoldása

\begin{matrix} f_{1} = \frac{h^{2}}{4 r} \cdot \frac{cos α}{sin α} [sin^{2} α - {(\frac{y}{h})}^{2} \frac{ϱ_{v}}{ϱ}] . \end{matrix}

45^{\circ} < α < 90^{\circ}, 0 < y < 2 r

intervallumban

f_{1} ≧ 0

mindig teljesül:

\begin{matrix} f_{2} = f_{1} \cdot sin α \cdot \frac{1}{cos β}, \\ h = \frac{y}{sin α} \cdot \frac{ϱ_{v}}{ϱ} + f_{1} \cdot cos α + f_{1} \cdot sin α \cdot tg β, \\ tg β = \frac{h - \frac{y}{sin α} \cdot \frac{ϱ_{v}}{ϱ} - f_{1} \cdot cos α}{f_{1} \cdot sin α} . \end{matrix}

- \frac{1}{2} ≦ ctg β ≦ \frac{1}{2}

és

F_{2}

miatt nem engedjük meg a

0^{\circ}

-nál kisebb és

180^{\circ}

-nál nagyobb szögeket. Így

β

-ra a megengedett intervallum 63,4

^{\circ} -

116,6

^{\circ}

f_{1} ≧ 0

miatt ebből is ki kell zárni a

90^{\circ}

-nál nagyobb szögeket.

\begin{matrix} ctg β = \frac{f_{1} sin α}{h - \frac{y}{sin α} \cdot \frac{ϱ_{v}}{ϱ} - f_{1} cos α}, \\ ctg β = \frac{1}{2} = \frac{f_{1} sin α}{h - \frac{y}{sin α} \cdot \frac{ϱ_{v}}{ϱ} - f_{1} cos α} . \end{matrix}

Az ebből meghatározott

y (α)

-nál nagyobb vízmagasság esetén a rúd megcsúszik és csak a sarokban áll meg:

\begin{matrix} \frac{h}{2} - \frac{y}{2 sin α} \cdot \frac{ϱ_{v}}{ϱ} = f_{1} (sin α + \frac{cos α}{2}), \\ \frac{h}{2} - \frac{y}{2 sin α} \cdot \frac{ϱ_{v}}{ϱ} = \frac{h^{2}}{4 r} \frac{cos α}{sin α} (sin α + \frac{cos α}{2}) [sin^{2} α - {(\frac{y}{h})}^{2} \frac{ϱ_{v}}{ϱ}], \\ y^{2} \cdot \frac{1}{h^{2}} \cdot \frac{ϱ_{v}}{ϱ} \cdot \frac{h^{2}}{4 r} \cdot \frac{cos α}{sin α} (sin α + \frac{cos α}{2}) - y \frac{1}{2 sin α} \frac{ϱ_{v}}{ϱ} + \frac{h}{2} - \\ - \frac{h^{2}}{4 r} \frac{cos α}{sin α} (sin α + \frac{cos α}{2}) sin^{2} α = 0. \end{matrix}

Ennek a másodfokú egyenletnek a gyökei adják meg azt a

h^{2}

magasságot, amelynél egy adott

α

helyzet már nem stabil és a rúd a sarokba csúszik.

\begin{matrix} y = 0 -nál α = 63, 67^{\circ} . \end{matrix}

Ennél kisebb kezdeti

α

esetén már a betöltés előtt a sarokba csúszik a rúd.
Most vizsgáljuk az (1

'

, 2

'

, 3

'

);

y > 2 r (1 - tg α)

által meghatározott egyensúlyi helyzeteket.

\begin{matrix} f_{1} = \frac{h^{2}}{4 r} cos^{2} α \cdot [1 - {(\frac{y - 2 r (1 - tg α)}{h \cdot sin α})}^{2} \frac{ϱ_{v}}{ϱ}] . \end{matrix}

0 < α < 45^{\circ}

0 < y < 8

2 r (1 - tg α) < y

intervallumban ez a kifejezés pozitív, így

f_{1} ≦ 0

mindig teljesül,

\begin{matrix} f_{2} = f_{1} \cdot sin α \cdot \frac{1}{cos β} -t  (2')-be helyettesítve \\ h = \frac{y - 2 r (1 - tg α)}{sin α} \cdot \frac{ϱ_{v}}{ϱ} + f_{1} \cdot cos α + f_{1} \cdot sin α \cdot tg β, \\ tg β = \frac{h - \frac{y - 2 r (1 - tg α)}{sin α} \cdot \frac{ϱ_{v}}{ϱ} - f_{1} cos α}{f_{1} \cdot sin α} . \end{matrix}

A megkötések

β

-ra :

\begin{matrix} - \frac{1}{2} ≦ tg β ≦ \frac{1}{2}, azaz - 26, 6^{\circ} ≦ β ≦ 26, 6^{\circ} \end{matrix}

és

- 90^{\circ} ≦ β ≦ 90^{\circ}

, mert a fal támaszerőt fejt ki. Mindez csak

y ≦ 2 r (1 - tg α)

esetén igaz.
A megcsúszás határesetében tg

β = \frac{1}{2}

vagy tg

β = - \frac{1}{2} .

\begin{matrix} \pm \frac{1}{2} = \frac{h - \frac{y - 2 r (1 - tg α)}{sin α} \cdot \frac{ϱ_{v}}{ϱ} - f_{1} cos α}{f_{1} sin α}, \\ f_{1} (cos α \pm \frac{sin α}{2}) = h - \frac{y - 2 r (1 - tg α)}{sin α} \cdot \frac{ϱ_{v}}{ϱ}, \\ \frac{h^{2}}{4 r} cos^{2} α [1 - {(\frac{y - 2 r (1 - tg α)}{h \cdot sin α})}^{2} \cdot \frac{ϱ_{v}}{ϱ}] (cos α \pm \frac{sin α}{2}) = \\ = h - \frac{y - 2 r (1 - tg α)}{sin α} \cdot \frac{ϱ_{v}}{ϱ}, \\ y^{2} \cdot \frac{h^{2}}{4 r} cos^{2} α \cdot \frac{ϱ_{v}}{ϱ sin^{2} α \cdot h^{2}} (cos α \pm \frac{sin α}{2}) - \\ - y [\frac{1}{sin α} \cdot \frac{ϱ_{v}}{ϱ} + cos^{2} α \cdot \frac{ϱ_{v}}{ϱ} \cdot \frac{(1 - tg α)}{sin^{2} α} \cdot (cos α \pm \frac{sin α}{2})] + h + \frac{2 r (1 - tg α)}{sin α} \cdot \frac{ϱ_{v}}{ϱ} - \\ - \frac{h^{2}}{4 r} \cdot cos^{2} α [1 - \frac{ϱ_{v}}{ϱ} \cdot \frac{4 r^{2} {(1 - tg α)}^{2}}{h^{2} \cdot sin^{2} α}] \cdot (cos α \pm \frac{sin α}{2}) = 0. \end{matrix}

Ennek a másodfokú egyenletnek a gyökei adják meg azokat a szögtartományokat, ahol lehetséges az egyensúly, feltéve, hogy vannak ilyen gyökök és a vízszint magasabban van a pálca végénél.
Ha a vízszint alacsonyabban van, mint a pálca vége, akkor (1

''

, 2

''

, 3

''

)-ből

\begin{matrix} h = f_{1} \cdot cos α + f_{1} sin α \cdot tg β, \\ tg β = \frac{h - f_{1} \cdot cos α}{f_{1} \cdot sin α} = \frac{h}{\frac{h^{2}}{4 r} \cdot cos^{2} α \cdot sin α} - \frac{cos α}{sin α}, \\ tg β = \frac{4 r}{h cos^{2} α \cdot sin α} - \frac{cos α}{sin α}, \\ tg β = \pm 1 -ből ctg α (\frac{8}{9} \frac{1}{cos^{3} α} - 1) = \pm \frac{1}{2} . \end{matrix}

Ennek numerikus megoldásából

\begin{matrix} + \frac{1}{2} : α_{1} = 29, 91^{\circ}, \\ - \frac{1}{2} : α_{2} = 8, 89^{\circ} . \end{matrix}

Azaz

α_{1}

-nél nagyobb szög esetén a pálca a falnál lecsúszik,

α_{2}

-nél kisebb szög esetén pedig kiborul.
Vizsgáljuk az

α = 45^{\circ}

-os helyeket!

\begin{matrix} sin 45^{\circ} = cos 45^{\circ} = \frac{1}{\sqrt[]{2}}, tg 45^{\circ} = 1. \end{matrix}

Ezt a helyzetet nem tekinthetjük az 1. ábra határesetének, nem feltételezhetjük, hogy a rúd csak az alsó lappal érintkezik.
Ha a 2. ábra határesetének tekintjük, azaz feltételezzük, hogy a rúd csak az oldalsó lappal érintkezik, a következőkre jutunk a

tg α = \pm \frac{1}{2}

-re adódó másodfokú egyenletből:

\begin{matrix} y^{2} \cdot \frac{1}{4 r} \cdot \frac{ϱ_{v}}{ϱ} (\frac{1}{\sqrt[]{2}} \pm \frac{1}{2 \sqrt[]{2}}) + \\ + y [\sqrt[]{2} \frac{ϱ_{v}}{ϱ}] + h - \frac{h^{2}}{4 r} \cdot \frac{1}{2} \cdot (\frac{1}{\sqrt[]{2}} \pm \frac{1}{2 \sqrt[]{2}}) = 0. \end{matrix}

(Sok tag esik ki az

1 - tg α = 0

miatt.)

\begin{matrix} y^{2} \cdot \frac{1}{16} \cdot \frac{8}{5} (1 \pm \frac{1}{2}) - y \cdot 2 \cdot \frac{8}{5} + \sqrt[]{2} \cdot 18 - \frac{18 \cdot 18}{16} \cdot \frac{1}{2} (1 \pm \frac{1}{2}) = 0, \\ y^{2} \cdot \frac{1}{10} \cdot (1 \pm \frac{1}{2}) - y \cdot \frac{16}{5} + [18 \cdot \sqrt[]{2} - \frac{81}{8} \cdot (1 \pm \frac{1}{2})] = 0. \\ y_{1,2} = \frac{\frac{16}{5} \pm \sqrt[]{{(\frac{16}{5})}^{2} - 4 \cdot \frac{1}{10} \cdot \frac{3}{2} + 18 \cdot 2 - \frac{81}{8} \cdot \frac{3}{2}}}{2 \cdot \frac{1}{10} \cdot \frac{3}{2}} < \binom{3, 934,}{17, 399.} \\ y_{3,4} = \frac{\frac{16}{5} \pm \sqrt[]{{(\frac{16}{5})}^{2} - 4 \cdot \frac{1}{10} \cdot \frac{1}{2} + 18 \sqrt[]{2} - \frac{81}{8} \cdot \frac{1}{2}}}{2 \cdot \frac{1}{10} \cdot \frac{1}{2}} < \binom{7, 178,}{56, 822.} \end{matrix}

Ez azt jelenti, hogy

y = 3, 934

cm-nél még nem elég a függőleges fal támasza, visszacsúszik a pálca az alaplapra is,

y = 7, 178

cm-nél pedig a

45^{\circ}

-os helyzetéből a rúd felcsúszik a falon. (Feltéve, hogy addig külső kényszerrel ott tartottuk.)
Tehát a pálca

45^{\circ}

-os helyzetében

3, 934

cm vízmagasságig nem lehet úgy, hogy csak az alaplapra vagy csak a falra támaszkodjon.
Azaz bármely vízmagassághoz és

45^{\circ}

-tól különböző helyzethez meg tudjuk mondani, hogy egyensúlyi helyzet vagy sem, s azt is

ctg α

ill.

tg α

alapján, hogy a súrlódási erő melyik irányban nem volt elegendő az egyensúly megtartásához, a rúd milyen irányban mozdult el.
Ahhoz azonban, hogy valamit tudjunk mondani a pálca

α = 45^{\circ}

-os viselkedéséről, a sarok alakjáról kellene többet tudnunk.
Ez a feladat egy egész problémakör. Egészen másként kell hozzáfogni a megoldásához, ha a saroknak a 3. a) ábra vagy a 3. b) ábra szerinti alakja van. A rúd vastagságának elhanyagolásával is csínján kell bánni.

3.a ábra

3.b ábra

Ezért ez a megoldás nem is lehetett más, csak útmutató.