Kezdőlap


Feladat:	2039. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Danyi András
Füzet:	1986/május, 227 - 228. oldal		PDF \| MathML
Témakör(ök):	Kepler III. törvénye, Mesterséges holdak, Feladat
Hivatkozás(ok):	Feladatok: 1985/május: 2039. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A lemaradó űrhajónak csökkenteni kell a sebességét ‐ ezt nevezik asztronautikai paradoxonnak. Ahhoz, hogy az $A$ űrhajó pontosan egy körülfordulás után utolérje a $B$ űrhajót, keringési idejét $\frac{2 π - φ}{2 π}$ -szeresére kell csökkenteni. Kepler III. törvénye szerint ezt úgy érheti el, hogy a sebességét csökkentve egy

\begin{matrix} α = R {(1 - \frac{φ}{2 π})}^{2 / 3} \end{matrix}

félnagytengelyű ellipszispályára áll (1. ábra, I. pálya).

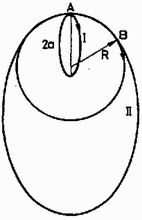1. ábra

Az ellipszispályán keringő űrhajó

v

pillanatnyi sebessége a következőképpen függ a középponttól mért

r

távolságtól:

\begin{matrix} v = \sqrt[]{γ M (\frac{2}{r} - \frac{1}{a})}, \end{matrix}

ahol

M

a vonzó égitest tömege,

γ

a gravitációs állandó,

a

a nagytengely fele. A formula megtalálható a Függvénytáblázatban és levezethető a Kepler-törvényekből. A kör- és az ellipszispálya adatait behelyettesítve megkapjuk az

A

űrhajó manőver előtti

v_{A_{1}}

és utáni

(v_{A_{2}})

sebességének nagyságát. (Az

A

űrhajó a manőver előtt a

B

űrhajóval egyező

v_{B}

sebességgel halad.)

\begin{matrix} v_{A_{1}} = \sqrt[]{\frac{M γ}{R}} = & v_{B}, \\ v_{A_{2}} = \sqrt[]{\frac{M γ}{R} [2 - {(1 - \frac{φ}{2 π})}^{- 2 / 3}]} = & v_{B} \sqrt[]{2 - {(1 - \frac{φ}{2 π})}^{- 2 / 3}} . \end{matrix}

A

-nak, miután utolérte

B

-t, vissza kell állni a körpályára, vagyis újból

v_{B}

sebességre kell gyorsítani. Ez a manőver addig kivitelezhető, ameddig

\begin{matrix} 2 - {(1 - \frac{φ}{2 π})}^{- 2 / 3} ≧ 0, \end{matrix}

azaz

\begin{matrix} φ ≦ 2 π (1 - 2^{- 3 / 2}) = 4,062 = 231, 7^{\circ} . \end{matrix}

A

űrhajó úgy is utolérheti

B

-t, hogy keringési idejét

\frac{4 π - φ}{2 π}

-szeresére növeli. Ilyenkor a találkozásig a

B

űrhajó több mint egy teljes kört tesz meg (1. ábra, II. pálya). A szükséges új sebességet ugyanúgy számítjuk ki, mint az előző manőver esetén; az eredmény:

\begin{matrix} v_{A_{2}} = v_{B} \sqrt[]{2 - {(2 - \frac{φ}{2 π})}^{- 2 / 3}} . \end{matrix}

Ez a manőver bármekkora

φ

esetén végrehajtható. Az űrhajós azt a megoldást választja, amely során kevesebb üzemanyagot kell felhasználni.

Δ v

sebességváltozás

Δ v m / V

tömegű üzemanyagot igényel (

m

az űrhajó tömege,

V

a kiáramló hajtóanyag sebessége). A szükséges üzemanyag tehát:

\begin{matrix} μ = 2 (m / V) | v_{A_{2}} - v_{B} |; \end{matrix}

(kétszer kellett sebességet megváltoztatni). A 2. ábrán

φ

függvényében ábrázoltuk

μ

-t (I és II görbék). Látható, hogy

φ = 1,8435 = 105, 6^{\circ}

-ig az első, ennél nagyobb szögek esetén a második manőver a gazdaságosabb.

Megjegyzés. A 2. ábrán ábrázoltuk egy olyan manővernek az üzemanyag-szükségletét is, amikor az űrhajó megnöveli sebességét, de egy kifelé irányított hajtóművel végig körpályán tartja az űrhajót (III. görbe). Látható, hogy az elhasznált hajtóanyag ilyenkor többszöröse a megoldásban bemutatott módszerek szükségletének. (Nem biztos viszont, hogy azok valóban a leggazdaságosabb megoldások.)

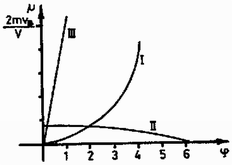2. ábra