Kezdőlap


Feladat:	1975. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csató János , Fülöp Tamás , Kaiser András , Sipos István
Füzet:	1985/május, 236 - 238. oldal		PDF \| MathML
Témakör(ök):	Steiner-tétel, Fizikai inga, Tömegközéppont helye, Feladat
Hivatkozás(ok):	Feladatok: 1984/november: 1975. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Számítsuk ki egy tetszőleges hosszúságú, felezőpontjában alátámasztott karikadarab lengésidejét (1. ábra) !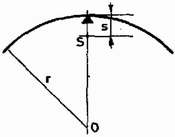

1. ábra

Egy fizikai inga lengésideje:

\begin{matrix} T = 2 π \sqrt[]{\frac{Θ}{M g s}}, \end{matrix}

ahol

Θ

az alátámasztási pontra vonatkozó tehetetlenségi nyomaték,

M

az inga tömege,

s

a súlypont és az alátámasztási pont távolsága,

g

pedig a nehézségi gyorsulás.

Θ

-t a Steiner-tétel kétszeri alkalmazásával kaphatjuk meg. A kör középpontjára vonatkozó tehetetlenségi nyomaték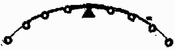

\begin{matrix} Θ_{0} = M r^{2}, \end{matrix}

ahol

r

a kör sugara. A súlypontra vonatkozó tehetetlenségi nyomaték

\begin{matrix} Θ_{s} = Θ_{0} - M {(r - s)}^{2}, \end{matrix}

az alátámasztási pontra vonatkozó tehetetlenségi nyomaték:

\begin{matrix} Θ = Θ_{s} + M s^{2} = 2 M r s . \end{matrix}

Ezt behelyettesítve a lengésidő képletébe

\begin{matrix} T = 2 π \sqrt[]{\frac{2 M r s}{M g s}} = 2 π \sqrt[]{\frac{2 r}{g}}, \end{matrix}

tehát

T

csak a karika sugarától függ, az ív hosszától nem, így a két karikadarab lengésideje egyenlő.

II. megoldás. Először számítsuk ki a következő test lengésidejét: Egy súlytalan drótból hajlított körívdarab két végére egyforma

m

tömegpontokat helyezünk. Az ívet a közepén támasztjuk alá (2. ábra).

2. ábra

Az alátámasztási pontra vonatkozó tehetetlenségi nyomaték

\begin{matrix} Θ = 2 m l^{2} = 2 m {(2 r sin α)}^{2} . \end{matrix}

A súlypont és az alátámasztási pont távolsága:

\begin{matrix} s = l sin α = 2 r sin^{2} α . \end{matrix}

Az inga lengésideje tehát

\begin{matrix} T = 2 π \sqrt[]{\frac{Θ}{2 m g s}} = 2 π \sqrt[]{\frac{2 r}{g}} . \end{matrix}

3. ábra

T

nem függ a körív középponti szögétől, csak a sugarától, tehát sok, különböző középponti szögű ívet (3. ábra) lengethetünk úgy, hogy a különböző ingák kitérési szögei minden időpillanatban megegyezzenek. A mozgáson az sem változtat, ha ezeket az ingákat összeerősítjük. Sok ilyen ingából összeállíthatunk olyan homogén tömegeloszlású gyűrűdarabokat, amilyenek a feladat szövegében szerepelnek, tehát ezek lengésideje is

T = 2 π \sqrt[]{\frac{2 r}{g}}

, az ív középponti szögétől függetlenül.

III. megoldás. Bontsuk fel a karikadarabot kis részekre, s ezeket helyettesítsük tömegközéppontokkal. A karikadarabnak a felezőpontjára vonatkozó tehetetlenségi nyomatékát közelíthetjük az egyes tömegpontok tehetetlenségi nyomatékának összegével:

\begin{matrix} Θ \approx \sum_{i}^{} m_{i} l_{i}^{2} = \sum_{i}^{} m_{i} 2 r y_{i} = 2 r \sum_{i}^{} m_{i} y_{i}, \end{matrix}

ahol

y_{i}

m_{i}

tömegpont

y

-koordinátája (4. ábra); ugyanis a derékszögű háromszög befogója az átfogónak és az átfogóra eső vetületének mértani közepe. A körív szimmetriája miatt nyilvánvaló, hogy súlypontja az

y

-tengelyre esik.

4. ábra

A súlypont

y

-koordinátája:

\begin{matrix} s = (\sum_{i}^{} m_{i} y_{i}) / (\sum_{i}^{} m_{i}) . \end{matrix}

Az inga tömege:

\begin{matrix} M = \sum_{i}^{} m_{i} . \end{matrix}

Számítsuk ki a lengésidőt

\begin{matrix} T = 2 π \sqrt[]{\frac{Θ}{M g s}} \approx 2 π \sqrt[]{\frac{2 r \sum_{i}^{} m_{i} y_{i}}{(\sum_{i}^{} m_{i}) g (\sum_{i}^{} m_{i} y_{i}) / (\sum_{i}^{} m_{i})}} = 2 π \sqrt[]{\frac{2 r}{g}} . \end{matrix}

A kapott érték független a karikadarab felbontásától, így a felosztás finomítása során adódó határérték is ugyanaz lesz,

T = 2 π \sqrt[]{\frac{2 r}{g}}

. Tehát a lengésidő egyenlő mindkét karikadarabra.

Megjegyzés. Az eredmény mindenféle tömegeloszlású (pl. változó vastagságú) körívre igaz, ha az alátámasztási pontot a súlyponton átmenő sugár végpontjába helyezzük (vagyis ha a súlypont az

y

-tengelyre esik).