Kezdőlap


Feladat:	1972. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh Péter
Füzet:	1985/május, 234 - 235. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Hajítások, Egyenletes körmozgás, Munkatétel, Feladat
Hivatkozás(ok):	Feladatok: 1984/november: 1972. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a testeket pontszerűnek ! Amíg a testek az 1. ábrán látható helyzetbe kerülnek, mindkét test gyorsulásának és sebességének nagysága $(v)$ egyenlő. Mivel súrlódás nincs, a munkatételből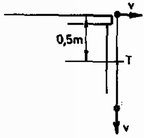

\begin{matrix} m g l = 2 \cdot (1 / 2) m v^{2}, v = \sqrt[]{g l} = 3, 16 m/s, (g = 10 {m/s}^{2}) . \end{matrix}

1. ábra

Amikor a felső test elhagyja az asztalt, függőleges sebessége nulla, az alsó testé pedig

v

. Ekkor egy ütközés játszódik le a két test között, amelyben az erőt a fonál közvetíti. Tételezzük fel, hogy a fonál mechanikai tulajdonságai olyanok, hogy ez az ütközés rugalmatlan, ellenkező esetben ugyanis a fonál belazul, és nagyon nehézzé válna a testek további mozgásának nyomonkövetése !
A testeket összekötő szakasz felezőpontjában található

T

tömegközéppont

v_{T} = (v_{x}, v_{y})

sebessége ekkor az impulzusmegmaradásból számolható:

\begin{matrix} v_{x} \cdot 2 m = m v + 0, v_{y} \cdot 2 m = 0 + m v, \end{matrix}

ebből

v_{x} = v / 2

v_{y} = v / 2

, így

v_{T}

nagysága

v / \sqrt[]{2}

, iránya a vízszintessel

- 45^{\circ}

-os szöget zár be.
A két testből álló rendszernek perdülete is van a tömegközéppont körül: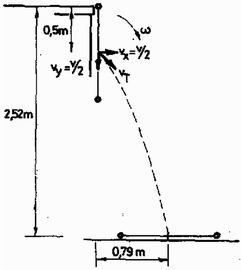

\begin{matrix} N = m v \cdot (l / 2) = Θ ω = 2 \cdot m {(l / 2)}^{2} ω, \end{matrix}

ebből

\begin{matrix} ω = v / l = \sqrt[]{g / l} . \end{matrix}

2. ábra

Az 1. ábrán látható helyzet után a tömegközéppont

v_{T}

kezdősebességgel, a ferde hajítás törvényei szerint mozog, miközben a testek állandó szögsebességgel körmozgást végeznek körülötte (2. ábra). A rendszer perdülete azért marad meg, mert a testekre ható nehézségi erő forgatónyomatéka nulla a tömegközéppontra nézve.
A kötél

π / 2

fordulat után kerül vízszintes helyzetbe, az ehhez szükséges idő:

\begin{matrix} t = \frac{π / 2}{ω} = \frac{π l}{2 v} = \frac{π}{2} \sqrt[]{\frac{l}{g}} = 0, 5 s . \end{matrix}

Ezalatt a tömegközéppont által függőlegesen megtett út:

\begin{matrix} y = v_{y} \cdot t + (g / 2) t^{2} = (v / 2) t + (g / 2) t^{2} . \end{matrix}

Az asztal szükséges magasságát úgy kapjuk meg, hogy

y

-hoz hozzáadjuk a tömegközéppont és az asztal szintjének

l / 2 = 0, 5 m

-es távolságát:

\begin{matrix} h = \frac{l}{2} + \frac{v}{2} t + \frac{g}{2} t^{2} = \frac{l}{2} + \frac{\sqrt[]{l g}}{2} \frac{π}{2} \sqrt[]{\frac{l}{g}} + \frac{g}{2} {(\frac{π}{2} \sqrt[]{\frac{l}{g}})}^{2} = l (\frac{1}{2} + \frac{π}{4} + \frac{π^{2}}{8}) = 2, 52 m . \end{matrix}

Könnyen ellenőrizhető, hogy az a hallgatólagos feltételezésünk, hogy az esés folyamán a kötél feszes, a mozgás során végig teljesül.
A

t = \frac{π}{2} \sqrt[]{\frac{l}{g}}

nem az egyetlen lehetséges megoldás, a

φ = \frac{π}{2} + k π = (2 k + 1) \frac{π}{2}

szögelforduláshoz tartozó megoldások is mind jók. Ennek megfelelően végtelen sok megoldás van:

\begin{matrix} h = l [\frac{1}{2} + \frac{π}{4} (2 k + 1) + \frac{π^{2}}{8} {(2 k + 1)}^{2}] . \end{matrix}

Az első néhány lehetséges asztalmagasság:

\begin{matrix} 2, 52 m, 13, 95 m, 35, 27 m . \end{matrix}

Ezek közül a legkisebb

2, 52 m

, de még ez sem normális asztalméret.