Kezdőlap


Feladat:	1958. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Béres Zoltán , Cserpák Edit , Csordás Zoltán Mihály , Drasny Gábor , Gutai Zsolt , Komorowicz Erzsébet , Kucsera Itala , Láng Róbert , László Ákos , Wiandt Tamás
Füzet:	1985/február, 88 - 89. oldal		PDF \| MathML
Témakör(ök):	Úszás, Kémiával kapcsolatos feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1984/október: 1958. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az areométer Arkhimédész törvénye értelmében különböző sűrűségű folyadékokba különböző mélyre merül. Legyen az areométer alsó részének térfogata $V_{0}$ , üvegcsövének keresztmetszete $A$ , hossza $h$ , az areométer tömege $m$ ! Feltételezhetjük, hogy az areométert úgy készítették, hogy az alsó része épp belemerül a tiszta vízbe. Arkhimédész törvénye miatt ekkor $V_{0} ϱ_{víz} g = m g$ . Határozzuk meg, hogy a vízbe merüléshez képest milyen $x$ mélységre merül egy $ϱ$ sűrűségű folyadékba (1. ábra)!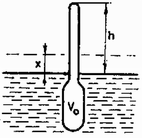

1. ábra

Az areométerre ható felhajtóerő egyensúlyt tart a nehézségi erővel így

\begin{matrix} (V_{0} + A \cdot x) \cdot ϱ \cdot g = m \cdot g, \end{matrix}

innen az előző összefüggéssel

\begin{matrix} x = \frac{V_{0}}{A} (\frac{ϱ_{víz}}{ϱ} - 1) . \end{matrix}

(1)

Ennek alapján tudunk olyan beosztást készíteni a csövön, amelyről a folyadék sűrűségét olvashatjuk le.
Ha megállapítjuk, hogy milyen összefüggés van az alkohol‐víz elegy sűrűsége és a keverék alkohol tömegkoncentrációja között, akkor a beosztást a tömegkoncentrációnak megfelelően is elkészíthetjük. A matematikai, fizikai és kémiai összefüggések c. tankönyv 189. oldalán található egy táblázat, amelyből leolvasható, mennyi a különböző arányú etilalkohol‐víz keveréknek a sűrűsége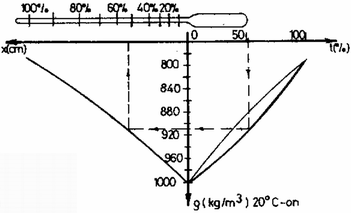

20^{\circ} C

-on.

2. ábra

Készítsük el a 2. ábrán látható grafikont! Ábrázoljuk először a tömegkoncentráció

(t)

függvényében a sűrűséget, majd az (1) összefüggés alapján a sűrűség függvényében az areométer csövének bemerülését (

x

-et)! Az így kapott grafikon alapján már elkészíthetjük a cső beosztását. (A szaggatott vonal az 50%-os koncentrációnak megfelelő beosztás elkészítését mutatja.)
Vizsgáljuk meg, hogyan függ a sűrűség a tömegkoncentrációtól! Öntsünk össze

m_{v}

tömegű vizet és

m_{a}

tömegű etilalkoholt. Ha feltételezzük, hogy összeöntéskor a víz és az alkohol térfogata összeadódik, akkor az elegy sűrűsége

\begin{matrix} ϱ = \frac{m_{v} + m_{a}}{(m_{v} / ϱ_{v}) + (m_{a} / ϱ_{a})} \end{matrix}

lesz (

ϱ_{v}

a víz,

ϱ_{a}

az alkohol sűrűsége).
Az elegy tömegkoncentrációja

t = \frac{m_{a}}{m_{v} + m_{a}} \cdot 100

, ezt felhasználva

\begin{matrix} ϱ = \frac{(m_{v} / m_{a}) + 1}{(m_{v} / ϱ_{v} m_{a}) + (1 / ϱ_{a})} = \frac{100 ϱ_{a} ϱ_{v}}{(ϱ_{v} - ϱ_{a}) t + 100 ϱ_{a}} \end{matrix}

Behelyettesítve

ϱ_{v}

és

ϱ_{a}

értékét

\begin{matrix} ϱ = \frac{10^{5}}{0, 267 t + 10^{2}} {kg/m}^{3} . \end{matrix}

(2)

Ha az így kapott sűrűséget

t

függvényében ábrázoljuk, a grafikonon a vékonyan húzott görbét kapjuk, ami eltér a táblázat alapján felrajzolt valódi görbétől. Ebből az következik, hogy víz és alkohol összeöntésekor az elegy térfogata kevesebb, mint az alkotórészek térfogatának összege.
Ha

ϱ

(2)-beli értéke alapján készítenénk a skálát, akkor az kb.

15 %

-os hibát okozna.