Kezdőlap


Feladat:	1921. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Antal Péter
Füzet:	1984/november, 421 - 422. oldal		PDF \| MathML
Témakör(ök):	Tömegközéppont helye, Feladat
Hivatkozás(ok):	Feladatok: 1984/március: 1921. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a szökőkutat folytonos tömegeloszlásúnak! Legyen egy pohár tömege $M$ , egy pohár pezsgőé $m$ ! Az oszlop magasságát a poharak számával fejezzük ki, legyen az $l$ $(l = 16)$ . Tegyük fel, hogy az $l$ pohár közül $x$ pohárban van pezsgő (l. ábra)! A rendszer $T$ tömegközéppontja olyan $y$ távolságra van az oszlop tetejétől, amelyre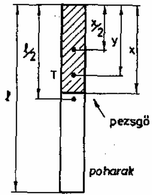

\begin{matrix} (y - \frac{x}{2}) x m = (\frac{l}{2} - y) l M, \end{matrix}

innen

\begin{matrix} y = \frac{M l^{2} + m x^{2}}{2 (M l + m x)} = \frac{l}{2} \cdot \frac{(M / m) + {(x / l)}^{2}}{(M / m) + (x / l)} . \end{matrix}

A feladat szerint ennek a kifejezésnek mint

x

függvényének az

x = 7

helyen van minimuma. Ha elvégezzük az

M / m = a

x / l = b

helyettesítést az

y = \frac{l}{2} \cdot \frac{a + b^{2}}{a + b}

kifejezést kapjuk, ennek mint

b

függvényének a minimuma a feladat szerint a

b = 7 / 16

helyen van. Tehát e kifejezés

b

szerinti deriváltja a

7 / 16

helyen nulla. A derivált értéke

\begin{matrix} y' (b) = \frac{l}{2} \cdot \frac{2 b (a + b) - (a + b^{2})}{{(a + b)}^{2},} \end{matrix}

így

\begin{matrix} \frac{l}{2} \cdot \frac{\frac{7}{8} (a + \frac{7}{16}) - [a + (\frac{16}{7})^{2}]}{{(a + \frac{7}{16})}^{2}} = 0, \end{matrix}

innen

\begin{matrix} a = \frac{49}{32}, azaz \frac{M}{m} = \frac{49}{32}, így M = 0,23 kg . \end{matrix}

Egy pezsgőspohár tömege tehát

0,23 kg

lehetett.

Megjegyzések. 1. Bármely más, egyébként helyes modell alapján becsült reális értéket elfogadtunk.
2. Helyesnek fogadtuk el az alábbi gondolatmenetet is: Legyen

x

tele pohár esetén

y (x)

a súlypont távolsága az oszlop tetejétől! Az

y (7) < y (8)

és

y (7) < y (6)

feltételek alapján egy felső és egy alsó korlátot kaphatunk egy pohár tömegére.