Feladat:	1864. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Jakab Dénes ,  Németh-Buhin Ákos
Füzet:	1984/február, 89 - 90. oldal		PDF  |  MathML
Témakör(ök):	Fizikai inga, Analógia alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1983/szeptember: 1864. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.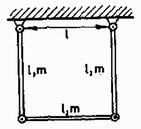 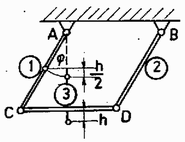    I. megoldás. Kitérítve, majd magára hagyva a rendszert, az összenergia, vagyis a helyzeti és a mozgási energiák összege állandó $\begin{array}{c}{\displaystyle E=E_h+E_m\mathrm{.}}\end{array}$ (1)     1. ábra   A helyzeti energia az 1. ábra alapján $\begin{array}{c}{\displaystyle E_h=mgh+mgh/2+mgh/2=2mgh\mathrm{,}}\end{array}$ ahol $h=l\left(1-\text{cos}\phi \right)$. Ha $\phi$ kicsi, $\text{cos}\phi \approx 1-{\phi }^2/2$. Ezek alapján $\begin{array}{c}{\displaystyle E_h\cong mgl{\phi }^2\mathrm{.}}\end{array}$ A rendszer mozgási energiája a három rúd mozgási energiájának összege: $\begin{array}{c}{\displaystyle E_m=E_m^1+E_m^2+E_m^3\mathrm{.}}\end{array}$ Legyen a rendszer pillanatnyi szögsebessége $\omega \left(t\right)$! A két szélső rúd mozgási energiája az $A$, illetve $B$ pont körüli forgás energiájával egyenlő: $\begin{array}{c}{\displaystyle E_m^1=E_m^2=\left(1/2\right)\Theta {\omega }^2\mathrm{,}}\end{array}$ ahol $\Theta =\left(1/3\right)m{l}^2$. Az alsó rúd minden pontja $l\omega$ sebességgel mozog, ezért $\begin{array}{c}{\displaystyle E_m^3=\left(1/2\right)m{\left(l\omega \right)}^2=\left(1/2\right)m{l}^2{\omega }^2\mathrm{.}}\end{array}$ Tehát $E_m=\left(5/6\right)m{l}^2{\omega }^2$. Tekintsünk egy $m\text{'}$ tömegű, $l\text{'}$ hosszúságú fonálingát, amelynek lengésideje, maximális szögkitérése és rezgési energiája megegyezik a három rúdból álló rendszerével! Ekkor a két rendszer maximális szögsebessége is megegyezik. Erre a fonálingára a fentiekhez hasonlóan $\begin{array}{c}{\displaystyle E_m=\left(m\text{'}/2\right){\left(\omega l\text{'}\right)}^2;E_h=m\text{'}gl\text{'}\left(1-\text{cos}\phi \right)\approx m\text{'}gl\text{'}{\phi }^2/2.}\end{array}$ A szélső helyzetben a két rendszer helyezeti energiája megegyezik: $\begin{array}{c}{\displaystyle m\text{'}gl\text{'}{\phi }_{\text{max}}^2/2=mgl{\phi }_{\text{max}}^2\mathrm{.}}\end{array}$ (1) A középső helyzetben a mozgási energiák egyenlők: $\begin{array}{c}{\displaystyle \left(m\text{'}/2\right){\left({\omega }_{\text{max}}l\text{'}\right)}^2=\left(5/6\right)m{l}^2{\omega }_{\text{max}}^2\mathrm{.}}\end{array}$ (2) A két egyenletből $\begin{array}{c}{\displaystyle l\text{'}=\left(5/6\right)l\mathrm{.}}\end{array}$ A fonálinga lengésidő képletét felhasználva kapjuk a keresett lengésidőt: $\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{l\text{'}}{g}}=2\pi \sqrt[]{\frac{5l}{6g}}\mathrm{.}}\end{array}$   II. megoldás. A rendszer vízszintes rúdjának minden pontja haladó mozgást végez, ugyanazzal a sebességgel, mint a $C$ és $D$ végpontok. 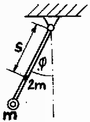    2. ábra   Az 1. és 2. rúd kitérése megegyezik, ezért rendszerünk helyettesíthető a 2. ábrán látható rendszerrel, amit egy $l$ hosszúságú, de $2m$ tömegű rúd, és a rúd végén található $m$ tömegű tömegpont alkot. A két rendszer lengésideje megegyezik. Ez utóbbira $T=2\pi \sqrt[]{\frac{\Theta }{Mgs}}$, ahol $\Theta$ a rendszer tehetetlenségi nyomatéka a forgáspontra nézve, $s$ a súlypont távolsága a felfüggesztéstől, $M$ pedig a rendszer össztömege. $\begin{array}{c}{\displaystyle \Theta =\left(1/3\right)\left(2m\right)l^2+m{l}^2\mathrm{,}s=\left(2/3\right)l\mathrm{,}M=3m\mathrm{.}}\end{array}$ Így $\begin{array}{c}{\displaystyle T=2\pi \sqrt[]{\frac{5l}{6g}}\mathrm{.}}\end{array}$