Feladat: 1844. fizika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Faragó Béla 
Füzet: 1983/december, 232 - 233. oldal  PDF  |  MathML 
Témakör(ök): Merev test egyensúlya, Feladat
Hivatkozás(ok):Feladatok: 1983/április: 1844. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.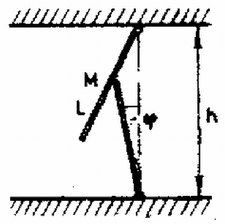

 

Jelölje K a két rúd közt ható erőt! Mivel nincs súrlódás, K merőleges a felső rúdra. Írjuk fel a forgatónyomatékok egyensúlyát a nyugalmi helyzetben az alsó, ill. a felső rúdra!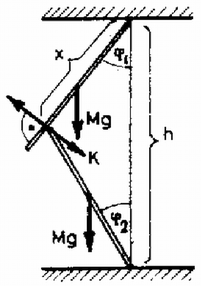
Mg(L/2)sinφ2=KLsin(π/2-φ1-φ2),(1)Mg(L/2)sinφ1=Kx.(2)


 


A szinusztételből
x/L=sinφ2/sinφ1,(3)
a koszinusztételből
h2=x2+L2-2Lxcos(π-φ1-φ2).(4)
A négy egyenlet rendezésével kiküszöbölhetjük φ1,φ2-t és K-t. Így a következő összefüggést kapjuk:
(xL)3+12(xL)2-12h2-L2L2=0.(5)
Adott h-hoz kiszámítható x és ebből a szögek.
 
Vizsgáljuk meg, mikor van megoldása az (5) egyenletnek!
Nyilván 0<x≦L.
Ebben az intervallumban az (xL)3+12(xL)2 kifejezés monoton növő függvénye x-nek, x=0-ban értéke nulla, tehát az (5) egyenletnek csak akkor létezhet megoldása, ha h>L. Az említett kifejezésnek maximuma van x=L-nél és ekkor értéke 3/2. Tehát ahhoz, hogy az (5) egyenletnek létezzék megoldása, teljesülnie kell a
32≧12h2-L2L2
egyenlőtlenségnek. Ez ekvivalens a h≦2L feltétellel.
 

Ahhoz tehát, hogy az (5) egyenletnek legyen olyan megoldása, amelyre 0<x≦L, szükséges, hogy teljesüljön az L<h≦2L feltétel. Könnyen belátható, hogy ez elégséges feltétel is. h=2L esetén azonban olyan megoldást kapunk, amelyre φ=0. Tehát a csuklók tetszőleges L<h<2L távolsága esetén az (1)-(4) egyenletrendszernek van megoldása, s így ekkor a pálcáknak van olyan egyensúlyi helyzete, amelyre 0<φ<π/2.
 

 Faragó Béla