Kezdőlap


Feladat:	1843. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Medgyesi Ferenc , Szolnoki Attila
Füzet:	1983/december, 231 - 232. oldal		PDF \| MathML
Témakör(ök):	Hajítások, Feladat
Hivatkozás(ok):	Feladatok: 1983/április: 1843. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először vizsgáljuk az $l = 0$ esetet! Tegyük fel, hogy a vízrészecskék $v$ kezdősebességgel hagyják el a tömlőt! A belocsolható maximális területet a ferde hajítás törvényei szabják meg. Különböző szög alatt locsolva, a belocsolható terület alakját a legmesszebb repülő vízrészecskék határozzák meg. Ennek kiszámolásához vegyünk fel egy koordinátarendszert a lejtőn (1. ábra)!

1. ábra

Legyen

O

a locsolás helye,

O D

a lejtő esésvonala, ami

α

szöget zár be a vízszintessel! Messük el a lejtőt az

O

ponton átmenő valamely függőleges síkkal Ennek a lejtő síkjával alkotott metszésvonala legyen

O C

! Ez az

O D

egyenessel zárjon be

β

szöget!
Vizsgáljuk az

O, C, B

pontokon átmenő síkban történő ferde hajítást! Számoljuk ki először ebben a síkban a "lejtő szögét'', vagyis

γ

-t!

\begin{matrix} \frac{O B}{O D} = sin α, \frac{O D}{O C} = cos β, \frac{O B}{O C} = sin γ . \end{matrix}

E három egyenletből

\begin{matrix} sin γ = sin α cos v β . \end{matrix}

(1)

Ezek után számoljuk ki azt, hogy egy

γ

szögű lejtőn milyen messzire lehet elhajítani egy testet

v

kezdősebességgel! A 2. ábra jelöléseivel írjuk fel a ferdehajítás mozgásegyenleteit!

\begin{matrix} x = (v sin δ) \cdot t, & (2) \\ y = (v cos δ) \cdot t - (g / 2) t^{2} & (3) \end{matrix}

A lejtő egyenlete

\begin{matrix} y = - (tg γ) x . \end{matrix}

(4)

(

δ

jelöli a hajítás függőlegessel bezárt szögét.)

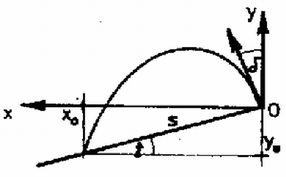2. ábra

A hajítás távolsága.

\begin{matrix} s = \sqrt[]{x^{2} + y^{2}} . \end{matrix}

(5)

A (2), (3) és (4) egyenletek segítségével, trigonometrikus átalakítások után

s

-re a következő kifejezést kapjuk:

\begin{matrix} s = \frac{v^{2}}{g} \end{matrix}

s

akkor maximális, ha

(2 δ - γ) = π / 2

vagy

(2 δ - γ) = - π / 2,

attól függően, hogy

sin γ

pozitív vagy negatív. Az egyik a felfelé, a másik a lefelé hajítás legtávolabbi pontját adja a

γ

hajlásszögű lejtőn.

\begin{matrix} s_{max} (lefelé) = \frac{v^{2}}{g cos^{2} γ} (1 + sin γ), \\ s_{max} (felfelé) = \frac{v^{2}}{g cos^{2} γ} (1 - sin γ) . \end{matrix}

(1) segítségével

\begin{matrix} s_{max} = \frac{v^{2}}{g} \cdot \frac{1}{1 \pm sin α cos β} . \end{matrix}

0 ≦ β < 2 π,

akkor elég a negatív előjelű tagot megtartani. Tehát

\begin{matrix} s_{max} = \frac{v^{2}}{g} \cdot \frac{1}{1 - sin α cos β .} \end{matrix}

(6)

Ez pedig egy ellipszis paraméteres egyenlete. (L. pl. Bronstejn-Szemengyajev: Matematikai zsebkönyv!)
Vizsgáljuk ezután az

l \neq 0

esetet!
Az előző pont érvelései alkalmazhatók annak figyelembevételével, hogy a cső vége az

O

ponttól

l

távolságra kerül, hiszen a feladat megfogalmazása szerint a cső végét nem emeljük fel a földről.
Ez annyiban módosítja a levezetést, hogy (6) helyett

\begin{matrix} S_{max} = \frac{v^{2}}{g} \cdot \frac{1}{1 - sin α cos β} + l . \end{matrix}

Ez a síkbeli polárkoordinátákban megadott egyenlet már nem ellipszis egyenlete, hanem egy negyedfokú görbéé.

3. ábra

Ha a

v = 10

m/s,

α = 45^{\circ},

numerikus értékekkel számolunk,

l = 0

és

l = 10

m esetén a belocsolható maximális területet a 3. ábra szemlélteti. A locsolócső a

P

pontban van rögzítve.

Szolnoki Attila (Nyíregyháza, Krúdy Gy. Gimn., II. o. t.)