Feladat:	1837. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Babarczy Emese ,  Megyesi Gábor
Füzet:	1983/december, 227 - 229. oldal		PDF  |  MathML
Témakör(ök):	Tökéletesen rugalmas ütközések, Síkinga, Nagy kitérítés, Feladat
Hivatkozás(ok):	Feladatok: 1983/március: 1837. fizika feladat

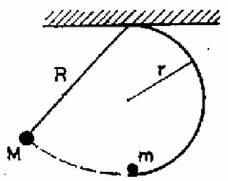
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Térítsük ki az $M$ tömegű testet alaphelyzetéből $\phi$ szöggel, és számítsuk ki a (tökéletesen rugalmas) ütközés utáni sebességeket! A mechanikai energiamegmaradás tétele alapján az $M$ tömegű test olyan $V$ sebességgel érkezik az $A$ pontba (1. az ábrát), amelyre nézve $\begin{array}{c}{\displaystyle MgR\left(1-\text{cos}\phi \right)=\left(1/2\right)M{V}^2\mathrm{.}}\end{array}$ (1) Ütközés közben a két test között csak belső erők hatnak, így az impulzusmegmaradás tétele szerint $\begin{array}{c}{\displaystyle MV=MU+mu}\end{array}$ (2) ahol $U\mathrm{,}$ ill. $u$ az $M\mathrm{,}$ ill. $m$ tömegű testek ütközés utáni sebessége.     Rugalmas ütközés esetén az energiamegmaradás tétele alapján $\begin{array}{c}{\displaystyle \left(1/2\right)M{V}^2=\left(1/2\right)M{U}^2+\left(1/2\right)m{u}^2\mathrm{.}}\end{array}$ (3) Az (1)-(3) egyenletekből $\begin{array}{c}{\displaystyle U=\frac{M-m}{M+m}V=\frac{M-m}{M+m}\sqrt[]{2gR\left(1-\text{cos}\phi \right)}\mathrm{,}}\end{array}$ (4) $\begin{array}{c}{\displaystyle u=\frac{2M}{M+m}V=\frac{2M}{M+m}\sqrt[]{2gR\left(1-\text{cos}\phi \right)}\mathrm{,}}\end{array}$ (5) Vizsgáljuk meg ezek után, mi a feltétele annak; hogy az $m$ tömegű test befussa a félkörívet! 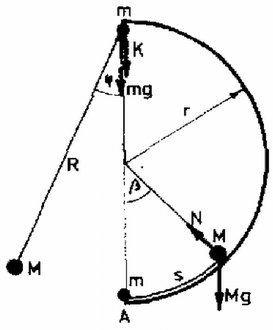Pályájának tetőpontján a $w$ sebességgel rendelkező $m$ tömegű testre az $mg$ nehézségi erő és a pálya $K$ kényszerereje hat: $\begin{array}{c}{\displaystyle K+mg=m{w}^2/r\mathrm{.}}\end{array}$ (6) Határesetben $K=\mathrm{0,}$ vagyis (6)-ból $\begin{array}{c}{\displaystyle w=\sqrt[]{gr}\mathrm{.}}\end{array}$ (7) Legalább ekkora sebességű kell, hogy legyen az $m$ tömegű test a pálya tetőpontján. Az $m$ tömegű testnek akkora $u$ sebességgel kell indulnia az $A$ pontból, hogy $\begin{array}{c}{\displaystyle \left(1/2\right)m{u}^2\geqq \left(1/2\right)m{w}^2+2mgr}\end{array}$ (8) legyen. Behelyettesítve a (8) egyenlőtlenségbe $u$ és $w$ (5), ill. (7) kifejezéseit, majd rendezve kapjuk, hogy $\begin{array}{c}{\displaystyle 0\leqq \text{cos}\phi \leqq 1-\frac{5}{8}\frac{r}{R}{\left(1+\frac{m}{M}\right)}^2\mathrm{,}}\end{array}$ (9 ) ahol a bal oldali egyenlőtlenség $0{}^{\circ }\leqq \phi \leqq {90}^{\circ }$ miatt teljesül. Adatainkkal a minimális kitérítés szögére (9)-ből$\left({90}^{\circ }\geqq \right)\phi \geqq 72\mathrm{,}{7}^{\circ }$ adódik. A minimális tömegarányt ugyancsak (9)-ből kapjuk $\phi ={90}^{\circ }$ (a legkedvezőbb eset) helyettesítéssel: $\begin{array}{c}{\displaystyle \frac{M}{m}\geqq \frac{1}{\sqrt[]{\frac{8}{5}\frac{R}{r}}-1}\mathrm{.}}\end{array}$ (10) Adatainkkal: $M/m\geqq 1\mathrm{,}27.$ A (10) egyenlőtlenségbőI leolvashatjuk még, hogy $R/r\leqq 5/8$ esetén $M$ és $m$ nem választható meg úgy, hogy az $m$ tömegű test befussa a, félkörívet. Végezetül számítsuk ki, hogy az ingatest legkisebb szükséges kitérítése $\left(\phi =72\mathrm{,}{7}^{\circ }\right)$ esetén mekkora utat fut be az $M$ tömegű test! Az ingatest ütközés utáni helyzetét a köríven jellemezzük a $\beta$ szöggel, sebessége legyen $W!$ Ekkor a sugárírányú erőkre $\begin{array}{c}{\displaystyle N-Mg\text{cos}\beta =M{W}^2/r\mathrm{,}}\end{array}$ (11) ahol $N$ jelöli a pálya kényszererejét. A test a körpályán addig emelkedik, amíg az alábbi feltételek egyike be nem következik:   $a)N=0\left(\beta \geqq {90}^{\circ }\right)$ vagy $b)W=0\left(\beta \leqq {90}^{\circ }\right)\mathrm{.}$   A test $W$ sebességét a mechanikai energiamegmaradás tételéből számolhatjuk: $\begin{array}{c}{\displaystyle \left(1/2\right)M{U}^2=\left(1/2\right)M{W}^2+Mgr\left(1-\text{cos}\beta \right)\mathrm{.}}\end{array}$ (12) A fenti egyenletbe $W=0$ értéket helyettesítve, valamint felhasználva (4)-et, adatainkkal $\left(\phi =72\mathrm{,}{7}^{\circ }\right)$ kapjuk, hogy a $W=0$ feltétel ${\beta }_{\text{max }}=32\mathrm{,}{5}^{\circ }$ esetén teljesül, vagyis a $b)$ eset valósul meg. Így az $M$ tömegű test által befutott ívhossz $\begin{array}{c}{\displaystyle s=r\beta \pi /{180}^{\circ }=0\mathrm{,}5\text{m}\cdot 32\mathrm{,}{5}^{\circ }\cdot \pi /{180}^{\circ }=0\mathrm{,}28\text{m}\mathrm{.}}\end{array}$    Babarczy Emese (Kalocsa, I. István Gimn., III. o. t.)