Feladat:	1836. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Rácz Attila
Füzet:	1983/november, 185 - 186. oldal		PDF  |  MathML
Témakör(ök):	Tömegközéppont megmaradása, A perdületmegmaradás törvénye, Egyéb úszás, Feladat
Hivatkozás(ok):	Feladatok: 1983/március: 1836. fizika feladat

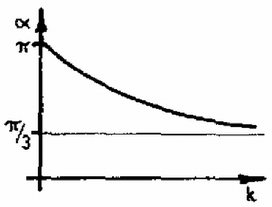
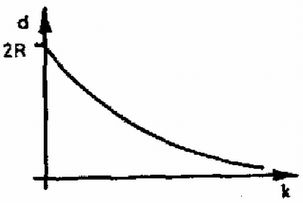
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.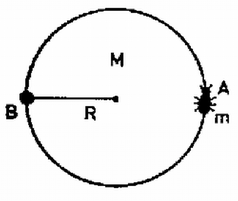 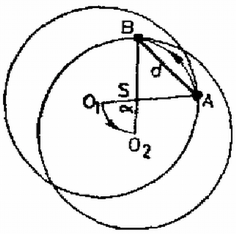  A korong mozgását két részből tehetjük össze: forog a tömegközéppontja körül, és a tömegközéppontja is elmozdul. Mivel nem hatnak vízszintes külső erők (a közegellenállást elhanyagoljuk), a bogár és a korong közös $S$ súlypontja a mozgás során egy helyben marad (l. az ábrát).     1. ábra     Az $S$ pont távolsága a korong $O$ súlypontjától $\left[m/\left(M+m\right)\right]R$, a bogártól $[M/\left(M+m\right]R$. Ez a két távolság állandó, így ez a két pont egy adott időpontban azonos $\omega$ szögsebességgel fog körpályán mozogni $S$ körül. Ezenkívül a korong $\Omega$ szögsebességgel foroghat a tömegközéppontja körül. A kezdeti impulzusmomentum zérus, és végig az is marad: $\begin{array}{c}{\displaystyle M{\left(\frac{m}{M+m}R\right)}^2\omega +m{\left(\frac{M}{M+m}R\right)}^2\omega +\frac{1}{2}M{R}^2\Omega =\mathrm{0,}}\end{array}$ ebből $\begin{array}{c}{\displaystyle \Omega =-\frac{2m}{M+m}\omega \mathrm{.}}\end{array}$ A bogárnak a koronghoz viszonyított szögsebessége: $\begin{array}{c}{\displaystyle \omega -\Omega =\frac{M+3m}{M+m}\omega \mathrm{.}}\end{array}$ Az azonos idő alatt történt szögelfordulások arányosak a szögsebességekkel, ha tehát a bogár a korong kerületén $\pi$ szöggel ment odébb, akkor a külső megfigyelőhöz képest a szögelfordulás $\begin{array}{c}{\displaystyle \alpha =\pi \frac{\omega }{\omega -\Omega }=\frac{M+m}{M+3m}\pi \mathrm{,}}\end{array}$ (és ez független attól, hogy a szögsebesség a mozgás során állandó volt-e vagy sem). Ezt a szögelfordulást a bogár egy $\frac{M}{M+m}R$ sugarú pályán teszi meg, az elmozdulás tehát $\begin{array}{c}{\displaystyle d=2\frac{M}{M+m}R\text{sin}\left(\frac{\pi }{2}\frac{M+m}{M+3M}\right)\mathrm{.}}\end{array}$ A különféle esetek áttekinthetőbbek, ha ábrázoljuk $\alpha$-t és $d$-t $m/M=k$ függvényében (2‐3. ábra).   2. ábra   3. ábra Ha $k\ll 1$ (a bogár tömege igen kicsi), a korong gyakorlatilag egy helyben marad: $\alpha =\pi$, $d=2R$. A másik határeset az, amikor a korong tömege a sokkal kisebb: $k\gg 1$. Ekkor a bogár marad egy helyben, csak hajtja maga alatt a korongot, aminek a középpontja a $B$ pontba érkezésekor $\pi /3={60}^{\circ }$-kal kerüli meg a bogarat.    Rácz Attila (Sopron, Berzsenyi D. Gimn., III. o. t.)