Feladat:	1799. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dobos Borbála ,  Tóth Árpád
Füzet:	1983/március, 139 - 140. oldal		PDF  |  MathML
Témakör(ök):	Egyenletes mozgás (Egyenes vonalú mozgások), Feladat
Hivatkozás(ok):	Feladatok: 1982/október: 1799. fizika feladat

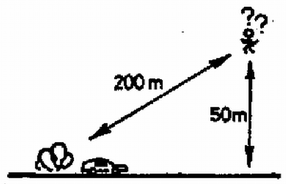
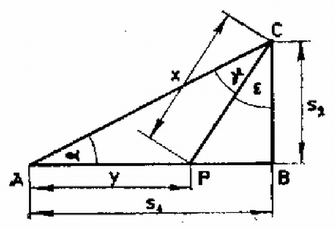
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Jelölje $P$ azt a pontot, ahol a gyalogos és az autó találkozik. Legyen $t$ az indulástól a találkozásig eltelt idő, $x$ a gyalogos, $y$ az autó által megtett út (1. ábra). Ekkor $\begin{array}{c}{\displaystyle x=vt\mathrm{,}y=ut\mathrm{,}}\end{array}$ (1) ahol $v$ a gyalogos, $u$ az autó sebessége. Az ábrán jelölt $CBP$ háromszög derékszögű, így $\begin{array}{c}{\displaystyle x^2=s_2^2+{\left(s_1-y\right)}^2\mathrm{,}}\end{array}$ (2) ahol $s_2=50\text{ m}$, $s_1=\sqrt[]{{200}^2-{50}^2}\text{ m}=193\mathrm{,}6\text{ m}$.   Rendezve az (1), (2) összefüggéseket, és beírva az ismert adatokat, a következő egyenletet kapjuk: $\begin{array}{c}{\displaystyle {\left(3t\right)}^2={50}^2+{\left(\sqrt[]{375}\cdot 10-10t\right)}^2\mathrm{.}}\end{array}$ (3) Az egyenlet két megoldása $\begin{array}{c}{\displaystyle t_1=24\mathrm{,}9\text{ s}\mathrm{,}{t}_2=17\mathrm{,}6\text{ s}\mathrm{.}}\end{array}$ Ezekből meghatározható $x$ és $y$, ezek segítségével pedig a $CP$ és a függőleges által bezárt szög: $\begin{array}{c}{\displaystyle {\epsilon }_1={48}^{\circ }\mathrm{,}{\epsilon }_2=-{19}^{\circ }\mathrm{.}}\end{array}$ A legkisebb sebesség $\left(v_{\text{min}}\right)$ meghatározásához is az előző összefüggéseket használjuk. A gyalogos a találkozásig most $x\text{'}=v_{\text{min}}t$ utat tesz meg. A (3) egyenlet most a következőképpen módosul: $\begin{array}{c}{\displaystyle {\left(v_{\text{min}}t\right)}^2={50}^2+{\left(\sqrt[]{375}\cdot 10-10t\right)}^2\mathrm{.}}\end{array}$ (4) Ezt az egyenletet átrendezve a $\begin{array}{c}{\displaystyle t^2\left(100-v_{\text{min}}^2\right)-t\cdot 200\sqrt[]{375}+40000=0}\end{array}$ (5) egyenlethez jutunk. Olyan $v_{\text{min}}$ értéket keresünk, amely a lehető legkisebb $\left(0<v_{\text{min}}\leqq 3\text{ m/s}\right)$, de amely mellett még eléri a gyalogos az autót, vagyis van $t$-ben megoldása az (5) egyenletnek. Az (5) egyenlet bal oldalán álló másodfokú függvény képe egy parabola. Könnyen látható, hogy ha az (5)-beli függvény másodfokú tagjának együtthatójában $v_{\text{min}}$ értéke csökken, akkor a parabola minimumának értéke nő. Ezért a legkisebb $v_{\text{min}}$ érték, amely mellett még van gyöke az (5) egyenletnek, akkor adódik, amikor a minimum $0$. Ekkor az (5) egyenletnek egy gyöke van, azaz a diszkriminánsa nulla: $\begin{array}{c}{\displaystyle {10}^4\left[1500-16{\left(100-v_{\text{min}}\right)}^2\right]=0}\end{array}$ amiből $v_{\text{min}}=2\mathrm{,}5\text{ m/s}$. A gyalogosnak ekkor $\epsilon =14\mathrm{,}{5}^{\circ }$ irányban kell futnia.    Dobos Borbála (Szolnok, Verseghy F. Gimn., III. o. t.)   II. megoldás. Az előző megoldásban használt jelöléseket alkalmazva írjuk fel az $APC$ háromszögre a szinusz-tételt: $\begin{array}{c}{\displaystyle \frac{\text{sin}\alpha }{\text{sin}\gamma }=\frac{x}{y}=\frac{v}{u}\mathrm{.}}\end{array}$ (6) Innen $\gamma =\text{ arc }\text{sin}\left[\left(u/v\right)\text{sin}\alpha \right]$. Ennek segítségével az $\epsilon$ szög meghatározható. A (6) egyenletből $\begin{array}{c}{\displaystyle v=u\frac{\text{sin}\alpha }{\text{sin}\gamma }\mathrm{.}}\end{array}$ (7) $v$ értéke akkor minimális, ha a (7) összefüggés jobb oldalán álló kifejezés értéke minimális, azaz $\text{sin}\gamma$ értéke maximális, vagyis $\gamma ={90}^{\circ }$. Ekkor $v_{\text{min}}=u\text{sin}\alpha$, a futónak pedig az $AC$-re merőleges irányban kell futnia.    Tóth Árpád (Kecskemét, Katona J. Gimn., III. o. t.)