| Feladat: | 1772. fizika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Füzet: | 1982/november, 182 - 185. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Lencserendszerek, Vastag lencse, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1982/március: 1772. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A tárgyról az 1. lencse a képet alkotja, amit a 2. lencse mint (virtuális) tárgyat újra leképez, így a két lencséből álló optikai rendszer együttesen a képet hozza létre.  1. ábra Az 1. ábra jelöléseit alkalmazva a leképzési törvény szerint
esetén (2a)-t így is írhatjuk:
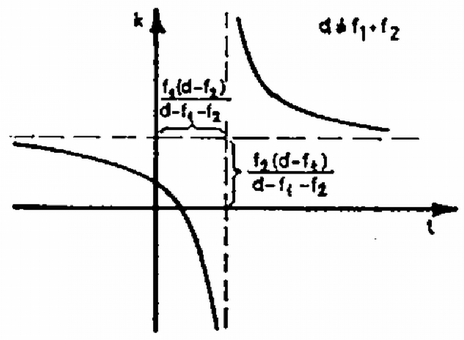 2. ábra 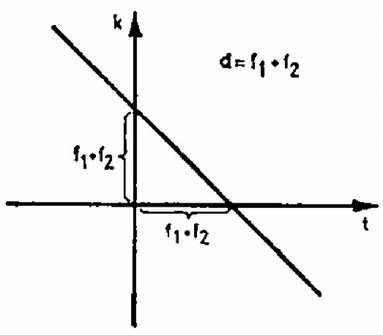 3. ábra Térjünk rá ezek után arra, hogyan alakíthatnánk át az összetartozó tárgy- és képtávolságokat leíró (2b) egyenletünket úgy, hogy a megszokott , vagy az ezzel ekvivalens (Newton-formula) alakú legyen. Ez utóbbi egyenlet alakját (2b)-vel összehasonlítva vegyük észre, hogy kétlencsés rendszerünk eredő fókusztávolságát a Tekintsük először a esetet, és vezessük be a
Foglalkozzunk ezek után a esettel. Az előbbiekhez hasonlóan az új tárgy- és képtávolságok
Zavaró azonban, hogy a fentiek alapján a rendszer fősíkjainak helyzete nem egyértelmű; attól függően, hogy melyik transzformációt alkalmazzuk, helyzetük különbözik. Arra gondolhatunk, hogy a (3a), (3b), ill. a (4a), (4b) egyenletek közül csak az egyik írja le helyesen a valóságos viszonyokat. Elvárjuk például, hogy esetén egy fókusztávolságú, vékony lencse jól ismert ill. leképezési törvényét kapjuk vissza (itt most és az 1. ábrán jelölt távolságokat jelöli), amelynek ‐ mint vékony lencsének ‐ fősíkjai egybeesnek. Valóban, ez a és a (3a), (3b) egyenletek alapján adódó , ill. fősíkok esetén láthatóan teljesül, míg a második transzformáció esetén nem. Ezért azt mondhatjuk, hogy (legalábbis a esetén) a rendszer viselkedését, ill. fősíkjainak helyzetét az Bebizonyítható, (pl. képszerkesztéssel), hogy ez esetén is igaz. Mi az oka tehát a látszólagos kétértelműségnek? Az egyszerűség kedvéért vizsgáljuk meg ezt egy fő fókusztávolságú vékony gyűjtőlencse példáján. A leképezési törvény alapján a lencsénk képalkotását az
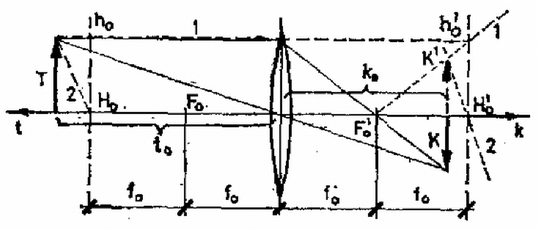 4. ábra
Láthatjuk, hogy a szerkesztés szerint is mind az (5), mind pedig a (6) összefüggés helyesen írja le az összetartozó kép- és tárgytávolságokat, de a (6) a valóságban keletkező képhez képest a fordított állású képet adja. Ebből az következik, hogy bár (6) matematikailag egyenértékű átírása (5)-nek, a valóságos képviszonyokat az (5) alapján végzett szerkesztéssel kapjuk. A példánkhoz hasonlóan ‐ kissé hosszadalmasabban ‐ belátható, hogy kétlencsés rendszerünk esetén is akkor kapunk helyes állású képet, ha szerkesztésünkben a (3a), (3b) transzformációkból adódó fősíkokat használjuk fel. |