| Feladat: | 1767. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Erdős László , Kovács Tamás , Simon Péter , Vereb György | ||
| Füzet: | 1982/november, 179 - 180. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Hajítások, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1982/március: 1767. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Vegyük fel a koordináta-rendszerünket úgy, hogy benne a lejtő a egyenletű sík legyen, az tengely legyen a feldobási ponton áthaladó esésvonal, az tengely pedig ugyanezen a ponton áthaladó szintvonal (l. az 1. ábrát). 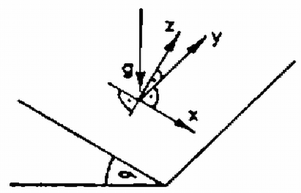 1. ábra Az origóból elindított testek mindenkor egy gömbfelületen helyezkednek el, amelynek középpontja -vel szabadon esik, sugara pedig szerint tágul ( időpillanatban történt a dobás). A gömb egyenlete:
Rögzített mellett keressük szélsőértékét! -nek egy másodfokú függvényéről van szó, amely a maximumát
Kovács Tamás (Debrecen, KLTE Gyak. Gimn., II. o. t.) dolgozata alapján II. megoldás. Vegyünk fel a lejtő síkjában egy polárkoordináta-rendszert, amelynek tengelye a dobási pontból induló esésvonal. Minden eldobott test pályájának a lejtő síkjára vett függőleges vetülete egy félegyenes, ennek polárszögét jelöljük -vel, a vízszintessel bezárt szögét -val (2. ábra). 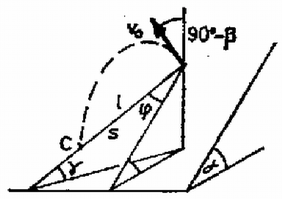 2. ábra Keressük az félegyenes mentén azt a legtávolabbi pontot, ahol leeshetnek a testek, ennél közelebb levő bármely pontra irányítható a dobás kisebb vagy nagyobb szögű hajítással. A és szög közötti összefüggés a Pitagorasz-tétel alapján:
A becsapódási pont távolsága -tól, a hajítási szög függvényében: (2. ábra)
Erdős László (Budapest, Berzsenyi D. Gimn., II. o. t.) |