| Feladat: | 1764. fizika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bognár György , Danyi Pál , Károlyi Gyula , Megyesi Gábor , Náray Miklós , Szállási Zoltán | ||
| Füzet: | 1982/november, 176 - 178. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Lencserendszerek, Mikroszkóp, Távcsövek, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1982/február: 1764. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Tekintsük az 1. ábrán vázolt esetet! 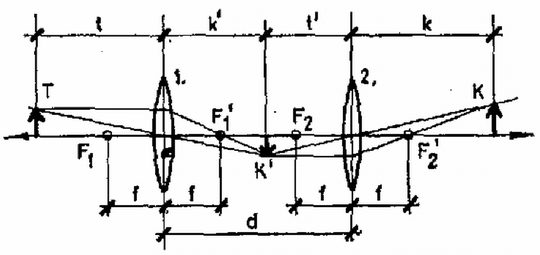 1. ábra Az 1. lencse által alkotott képet a 2. lencse újból leképezi. Az ismert lencse-törvény szerint
Vizsgáljuk meg ezután a kétlencsés rendszerünk leképezését leíró (2a) egyenletet! Leolvasható, hogy esetén
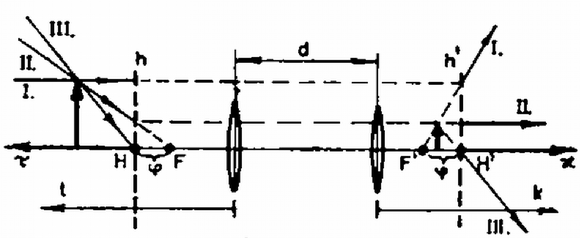 2. ábra
A fősíkok használatával a képszerkesztés is nagyon hasonló a vékony lencsénél megszokotthoz, ezt illusztrálja a három fő sugármenet felhasználásával a 2. ábra. 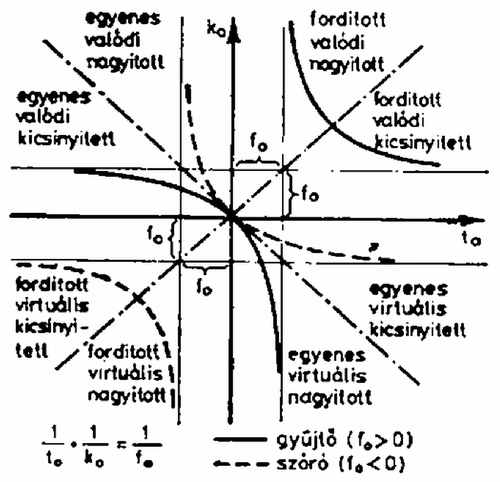 3. ábra Egy vékony lencse képalkotását tekinthetjük át a 3. ábrán, amelyen a koordináta-tengelyek és a velük -os szöget bezáró, az origón átmenő egyenesek által határolt síknyolcadokban futó görbe szakaszokhoz tartozó kép jellemzőit tüntettük fel. (Az adott lenesére vonatkozó adatokat , , -lal jelöltük.) Bár formailag (2c) is egy vékony lencse leképezését írja le, lényeges különbség az, hogy nem feltétlenül virtuális (ernyőn fel nem fogható) képet (tárgyat) jelent, hanem csak azt, hogy a kép (tárgy) a fősík mögött van. (Egy ideális vékony lencse két fősíkja egybeesik.) Hogy egy adott (ill. ) értékhez tartozó kép (ill. tárgy) látszólagos vagy sem, azt (ill. ) előjelének a (4a), (4b) alapján történő vizsgálatával dönthetjük el. A 4., 5., 6., 7. ábrán a paraméter különböző értékei mellett ábrázoltuk kétlencsés rendszerünk esetében az összetartozó tárgy- és képtávolságokat mind a (2c) egyenlet), mind pedig a (2a) egyenlet) koordináta-rendszerben. A két koordináta-rendszer egymáshoz viszonyított helyzetét a (4a), (4b) egyenletek jellemzik. Az ábrákról és előjelét leolvasva adódik, hogy a kép, ill. tárgy valódi vagy virtuális-e. A 3. ábra alapján a keletkező kép állását határozhatjuk meg. 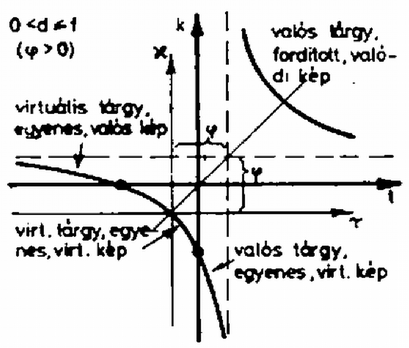 4. ábra 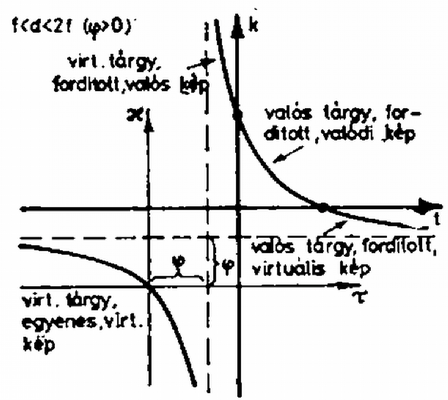 5. ábra 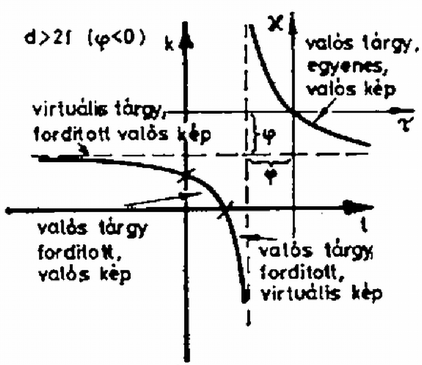 6. ábra 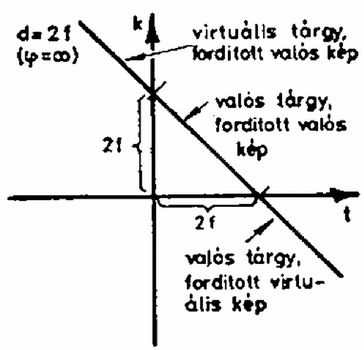 7. ábra Végül esetén egy közönséges gyújtótávolságú vékony lencsét kapunk, amelynek képalkotása jól ismert. |