Feladat:	1755. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Fodor Zoltán ,  Gyuricza Béla ,  Peták Tamás ,  Szövényi-Lux Márton ,  Szövényi-Lux Mátyás
Füzet:	1982/október, 92 - 93. oldal		PDF  |  MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Nyomóerő, kötélerő, Kúpinga, Egyéb matematikai inga, Centrifugális erő, Feladat
Hivatkozás(ok):	Feladatok: 1982/január: 1755. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.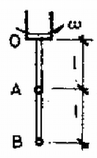 Megfelelően nagy szögsebességgel forgatva a rendszert, a pálcák a függőlegestől ${\phi }_1$ és ${\phi }_2$ szögekkel fognak kitérni. Írjuk fel ebben a helyzetben a golyók mozgásegyenletét (1. ábra)! Az $A$ tömegpontra az egyenletek: 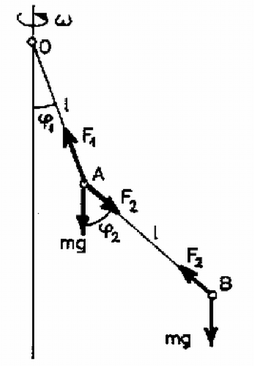  1. ábra   $\begin{array}{c}{\displaystyle F_1\text{cos}{\phi }_1-mg-F_2\text{cos}{\phi }_2=\mathrm{0,}}\end{array}$ (1) $\begin{array}{c}{\displaystyle F_1\text{sin}{\phi }_1-F_2\text{sin}{\phi }_2=ml{\omega }^2\text{sin}{\phi }_1;}\end{array}$ (2) a $B$ golyóra pedig $\begin{array}{c}{\displaystyle F_2\text{cos}{\phi }_2-mg=\mathrm{0,}}\end{array}$ (3) $\begin{array}{c}{\displaystyle F_2\text{sin}{\phi }_2=ml{\omega }^2\left(\text{sin}{\phi }_1+\text{sin}{\phi }_2\right)\mathrm{.}}\end{array}$ (4) A pálcákban ébredő $F_1$ és $F_2$ erőket kiküszöbölve az egyeletekből, valamint az $\alpha =l{\omega }^2/g$ új változót bevezetve az alábbi egyenletrendszert kapjuk ${\phi }_1$ és ${\phi }_2$-re: $\begin{array}{c}{\displaystyle 2\text{tg}{\phi }_1-\text{tg}{\phi }_2=\alpha \text{sin}{\phi }_1\mathrm{,}}\end{array}$ (5) $\begin{array}{c}{\displaystyle \text{tg}{\phi }_2=\alpha \left(\text{sin}{\phi }_1+\text{sin}{\phi }_2\right)\mathrm{.}}\end{array}$ (6) Ezekből az egyenletekből ${\phi }_1$ és ${\phi }_2$ explicit kifejezése reménytelenül bonyolult vállalkozás lenne. Bennünket azonban most csupán az érdekel, hogy mekkora $\alpha$ (ill. $\omega$) értéktől kezdve fogunk nullától különböző szögkitérést kapni. Ebben a határhelyzetben ${\phi }_1$ és ${\phi }_2$ kicsiny értékűek, így az (5) és a (6) egyenletekben a $\text{tg }\phi \approx \phi$ és a $\text{sin}\phi \approx \phi$ közelítések alkalmazhatók. Ennek felhasználásával $\alpha$-ra másodfokú egyenletet nyerünk: $\begin{array}{c}{\displaystyle {\alpha }^2-4\alpha +2=\mathrm{0,}}\end{array}$ amelynek kisebbik gyöke fogja a kritikus szögsebességértéket meghatározni: $\begin{array}{c}{\displaystyle {\omega }_{\text{<span style="font-style: italic;">kr</span>}}=\sqrt[]{\left(g/l\right)\left(2-\sqrt[]{2}\right)\mathrm{.}}}\end{array}$ A ${\phi }_1=0$, ${\phi }_2=0$ mindig megoldása az egyenleteknek. Belátható, hogy ha $\omega <{\omega }_{\text{<span style="font-style: italic;">kr</span>}}$, akkor a ${\phi }_1={\phi }_2=0$ stabil megoldás, míg ha $\omega <{\omega }_{\text{<span style="font-style: italic;">kr</span>}}$, akkor instabil, azaz bármilyen kis eltérés ettől a helyzettől már tovább téríti ki a pálcákat egészen addig, amíg a rendszer át nem megy az (5) és (6) egyenletekkel leírt helyzetbe. A stabilitás vizsgálatára használjunk $\omega$ szögsebességgel forgó koordinátarendszert! Ha az $m$ tömegek kicsit mozdulnak ki a tengelytől, akkor a helyzeti energia növekedése 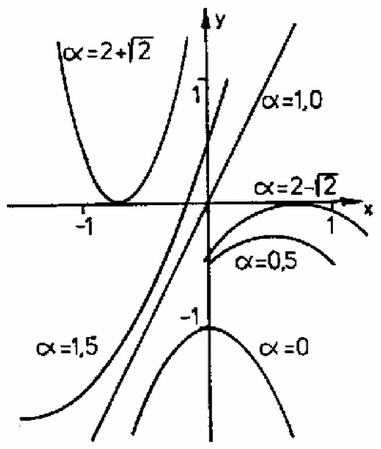$\begin{array}{c}{\displaystyle \Delta E_h=\frac{mgl}{2}\left(2{\phi }_1^2+{\phi }_2^2\right)\mathrm{.}}\end{array}$ Ezt a növekedést a centrifugális erők $\begin{array}{c}{\displaystyle \Delta W_{\text{<span style="font-style: italic;">cf</span>}}=\frac{m{\omega }^2{l}^2}{2}\left(2{\phi }_1^2+2{\phi }_1{\phi }_2+{\phi }_2^2\right)}\end{array}$ munkavégzése fedezheti (ez utóbbi a tömegek kinetikus energiája). Mindaddig, amíg különbségük ($\Delta E=\Delta W_{\text{<span style="font-style: italic;">cf</span>}}-\Delta E_h$) negatív, a ${\phi }_1={\phi }_2=0$ helyzet stabilis. Kis átlakítások után $\begin{array}{c}{\displaystyle y=2\left(\alpha -1\right)\cdot x^2+2\alpha x+\left(\alpha -1\right)}\end{array}$ (7) adódik, ahol $y=\frac{2\Delta E}{mgl{\phi }_2^2}$, $x=\frac{{\phi }_1}{{\phi }_2}$. A 2. ábra néhány $\alpha$ paraméter‐értékre feltünteti ezt a függvénykapcsolatot.   2. ábra 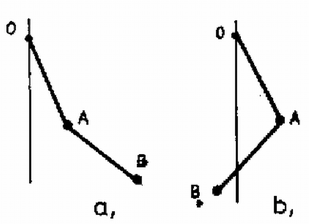    3. ábra   $\alpha <2-\sqrt[]{2}$ esetén minden $x$-re $y<0$, azaz a ${\phi }_1={\phi }_2=0$ helyzet stabilis. $\alpha \le 1\left(\omega \le \sqrt[]{\frac{g}{l}}\right)$ esetén csak pozitív $x$ értékeknél válhat $y$ (és így $\Delta E$) pozitívvá, azaz ${\phi }_1$ és ${\phi }_2$ azonos előjelűek: az egyensúlyi helyzet akkor valósulhat meg, ha a pálcák azonos irányban térnek ki (3a ábra). $\alpha >1$ esetén a ${\phi }_1={\phi }_2=0$ helyzetben bekövetkező zavar (perturbáció) mindkét stabil konfigurációt (3a és 3b ábrák) létrehozhatja.    Több dolgozat alapján