Kezdőlap


Feladat:	1748. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Szállási Zoltán
Füzet:	1982/április, 186 - 188. oldal		PDF \| MathML
Témakör(ök):	Coulomb-törvény, Megosztás, Feladat
Hivatkozás(ok):	Feladatok: 1981/december: 1748. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.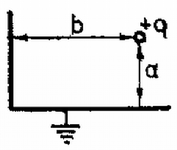

Először oldjunk meg egy egyszerűbb feladatot: "Egy végtelen kiterjedésű, földelt sík fémlemeztől

d

távolságra

q

nagyságú ponttöltést helyezünk el (1. ábra). Mekkora erő hat a töltésre?''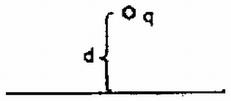

1. ábra

A két test között vonzóerő hat, mivel a fémlemez felületén a

q

töltés előjelével ellentétes előjelű indukált töltések jelennek meg (elektromos megosztás jelensége). A fémlemez felületén a töltéssűrűséget az határozza meg, hogy a fémlemez minden pontja azonos potenciálon van. Ez azért van így, mert a fémben szabad töltéshordozók vannak (elektronok), amelyek a fém belsejében a térerősség hatására gyorsulni kezdenek. Addig mozognak, amíg olyan tér nem alakul ki, amelynek erőssége a fémben mindenütt nulla, és a térerősségnek a fém felületén sincs a felülettel párhuzamos összetevője. Így a fém minden pontjában a potenciál azonos, másképpen szólva az erővonalak merőlegesen érik el a fém felületét. Vékony fémlemezek esetében azt szokás mondani, hogy a fém ekvipotenciális felület. Esetünkben a fémlemez földelt, így potenciálja nulla.
A fém felületén összegyűlt megosztott töltések összege éppen a

q

töltés mínusz egyszerese, azaz minden, a

q

ponttöltésből kiinduló erővonal a fémlemezen végződik. Ha meg tudjuk határozni a fémlemezen felhalmozott (egyelőre ismeretlen eloszlású)

- q

töltés terének térerősségét a

q

töltés helyén, akkor a keresett erőt is megkapjuk.
Ezt a töltéselrendezést azonban közvetlenül nagyon nehéz kiszámítani. A 1739. feladat megoldásában (l. a 181. oldalt) azonban láttuk, hogy az egymástól

2 d

távolságra levő

+ q

és

- q

ponttöltés között elhelyezkedő szimmetriasík éppen a nulla potenciálú ekvipotenciális felület, azaz ezen felületet minden erővonal merőlegesen metsz. Így, ha a két töltés közé a tükörsík helyére vékony, végtelen kiterjedésű sík fémlemezt helyezünk, a fémlemez belsejében a térerősség nulla, a fémlemezen kívüli tér pedig változatlan lesz. Az erővonalképet és a felületen megjelenő indukált (megosztott) töltéseket szemlélteti a

2 a

és

2 b

ábra a fémlemez behelyezése előtt és után.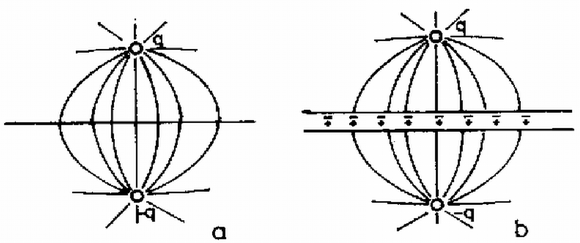

2. ábra

Ha a

2 b

ábrán látható elrendezést a fémlemez középsíkja mentén kettévágjuk, megkapjuk az abban a feladatban keresett erővonalképet, amely az 1. ábra elrendezésének felel meg (3. ábra).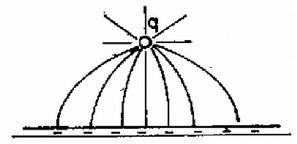

3. ábra

Ez a tér kielégíti azt a feltételt, hogy a fémlemez ekvipotenciális legyen, vagy más szóval azt, hogy az erővonalak merőlegesen érjék el a fém felületét. A fémlemezen levő töltések eloszlását is megkaphatjuk ebből a képből, de arra a kérdésre, hogy mekkora erő hat a

q

töltésre, a megosztással kialakult töltéseloszlás pontos ismerete nélkül is felelhetünk. A

q

nagyságú töltésre a fémlemez által ható erő megegyezik a

- q

nagyságú töltés által a

q

nagyságú töltésre ható erővel, azaz

\begin{matrix} F = \frac{1}{4 π ε_{0}} \cdot \frac{q^{2}}{4 d^{2}}, \end{matrix}

ahol

ε_{0}

a vákuum dielektromos állandója, az erő pedig vonzó irányú.
A most bemutatott tükrözéses módszer segítségével oldhatjuk meg a feladatban kitűzött problémát is. Keressünk olyan töltéselrendezéseket, amelyeknek a nulla potenciálhoz tartozó ekvipotenciális felülete éppen a két fémlemeznek megfelelő, egymásra merőleges sík. Mivel a megosztott töltések összege éppen

- q

, a "tükörtöltések'' összege is

- q

kell, hogy legyen, mivel az eredeti

q

töltés térnegyedében ezek terével helyettesítjük a fémlemezen levő töltések terét. Tükrözzük a két síkon a

q

nagyságú töltést. Az így kapott két

- q

nagyságú töltést még ki kell egészítenünk a két

- q

nagyságú töltés továbbtükrözésével kapott

+ q

töltéssel (4. ábra).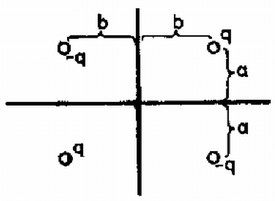

4. ábra

Az így kapott három tükörtöltés összege most valóban

- q

, még és az is teljesül, hogy ennek a négy töltésnek a nulla potenciálhoz tartozó ekvipotenciális felülete éppen a kívánt két, egymásra merőleges sík. Így

q

a töltésre ható kérdéses erő egyenlő a három tükörtöltés által kifejtett erők eredőjével.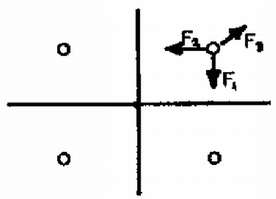

5. ábra

Az 5. ábra jelölései szerint

\begin{matrix} F_{1} = \frac{1}{4 π ε_{0}} \cdot \frac{q^{2}}{4 a^{2}}; F_{2} = \frac{1}{4 π ε_{0}} \cdot \frac{q^{2}}{4 b^{2}}; \\ F_{3} = \frac{1}{4 π ε_{0}} \frac{q^{2}}{4 (a^{2} + b^{2})}, \end{matrix}

azaz a

q

töltésre ható eredő erő vízszintes összetevője:

\begin{matrix} F_{v} = F_{2} - F_{3} \frac{b}{\sqrt[]{a^{2} + b^{2}}} = \frac{q^{2}}{16 π ε_{0}} (\frac{1}{b^{2}} - \frac{b}{{(a^{2} + b^{2})}^{3 / 2}}); \end{matrix}

a függőleges összetevője:

\begin{matrix} F_{f} = F_{1} - F_{3} \frac{a}{\sqrt[]{a^{2} + b^{2}}} = \frac{q^{2}}{16 π ε_{0}} (\frac{1}{a^{2}} - \frac{a}{{(a^{2} + b^{2})}^{3 / 2}}) . \end{matrix}

Szállási Zoltán (Esztergom, Dobó K. Gimn., IV. o. t.)