Feladat:	1746. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Vityi Péter
Füzet:	1982/május, 234 - 235. oldal		PDF  |  MathML
Témakör(ök):	Hajítások, Nagy kitérítés, Feladat
Hivatkozás(ok):	Feladatok: 1981/december: 1746. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.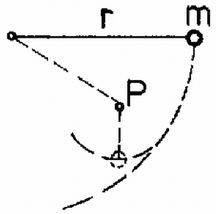 A tömegpont $A$-tól $B$-ig egy $O$ középpontú, $r$ sugarú, $B$-től $C$-ig egy $P$ középpontú, $r\text{'}$ sugarú köríven végez kényszermozgást (1. ábra). $C$-ben megszűnik a fonalat feszítő erő ‐ innen a pálya parabola alakban folytatódik, és ha jó helyre vertük be a szöget, éppen átmegy $P$-n. $C$-ben a centripetális erő egyenlő a tömegpont súlyának kötélirányú összetevőjével: 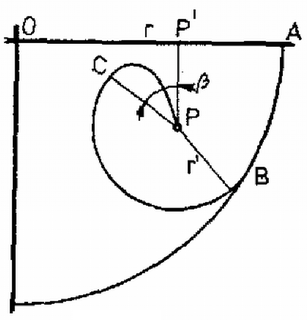$\begin{array}{c}{\displaystyle m{v}^2/r\text{'}=mg\text{cos}\beta }\end{array}$ (1) ($\beta$ a $CP$ szakasz függőlegessel bezárt szöge, $v$ a test sebessége $C$-ben). A $C$ pontból parabolapályán folytatja a tömegpont a mozgást. A parabolapálya akkor halad át a $P$ ponton, ha alkalmas $t$-re   1. ábra ${\displaystyle \begin{array}{cc}\hfill {\displaystyle r\text{'}\text{sin}\beta =v\left(\text{cos}\beta \right)t\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle r\text{'}\text{cos}\beta =\left(g/2\right)t^2-v\left(\text{sin}\beta \right)t\mathrm{.}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ Az (1), (2), (3) egyenletrendszerből a $\beta \mathrm{,}v$ ismeretlenek kiszámíthatók: $\begin{array}{c}{\displaystyle \text{cos}\beta =1/\sqrt[]{3}\mathrm{,}{v}^2=gr\text{'}/\sqrt[]{3}\mathrm{.}}\end{array}$ Vegyük fel ezután a 2. ábra szerinti derékszögű koordináta-rendszert ! 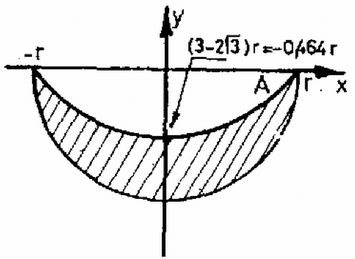  2. ábra Ebben $P$ koordinátái: $\left(x\mathrm{,}y\right)$. A $C$ pontban a test mozgási energiája a helyzeti energiájának megváltozásával egyenlő: $\begin{array}{c}{\displaystyle \left(1/2\right)m{v}^2=mg\left(-y-r\text{'}\text{cos}\beta \right)\mathrm{.}}\end{array}$ (4) Behelyettesítve $v^2$-et és $\text{cos}\beta$-t: $\begin{array}{c}{\displaystyle y=-\left(\sqrt[]{3}/2\right)r\text{'}\mathrm{.}}\end{array}$ (4') Az $x$, $y$, $r$ és $r\text{'}$ hosszúságok között létezik még egy összefüggés, az $OPP\text{'}$ háromszögre felírt Pitagorasz-tétel: $\begin{array}{c}{\displaystyle {\left(r-r\text{'}\right)}^2=x^2+y^2\mathrm{.}}\end{array}$ (5) A (4') ‐ (5) egyenletrendszerből kiküszöbölve $r\text{'}$-t, a 2. ábrán látható hiperbola egyenletét kapjuk: $\begin{array}{c}{\displaystyle \frac{{\left(y+2\sqrt[]{3}r\right)}^2}{{\left(3r\right)}^2}-\frac{x^2}{{\left(\sqrt[]{3}r\right)}^2}=1.}\end{array}$ A keresett mértani hely a hiperbolának a $\left(-r\mathrm{,}0\right)$ és $\left(r\mathrm{,}0\right)$ pontok közé eső szakasza. Az alatta levő bevonalkázott területre bevert szögeket mind megkerüli a tömegpont.    Vityi Péter (Budapest, Móricz Zs.Gimn., III. o. t.)  dolgozata alapján   Megjegyzés. Sok megoldó nem értette meg a feladatot, és lényegében a 1737. feladatot oldotta meg újra. Dolgozatukra így nem kaphattak pontot.