Kezdőlap


Feladat:	1739. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Drávucz Katalin
Füzet:	1982/április, 181 - 184. oldal		PDF \| MathML
Témakör(ök):	Coulomb-potenciál, Coulomb-energia, Feladat
Hivatkozás(ok):	Feladatok: 1981/november: 1739. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mielőtt a feladat megoldásához kezdenénk, vizsgáljuk meg egy $q$ ponttöltés ekvipotenciális felületeit. Tegyük fel, hogy a térben ezen ponttöltésen kívül más nincs is, azaz a töltés környezete vákuum. A potenciál a töltéstől $r$ távolságra

\begin{matrix} U (r) = \frac{1}{4 π ε_{0}} \frac{q}{r}, \end{matrix}

ahol

ε_{0}

a vákuum dielektromos állandója. Az ekvipotenciális felület egyenlete

\begin{matrix} U (r) = állandó \end{matrix}

amiből az

\begin{matrix} r = állandó \end{matrix}

feltétel adódik, ami egy olyan

r

sugarú gömb egyenlete, amelynek középpontjában van a töltés. Így a ponttöltés valamennyi ekvipotenciális felülete gömbfelület.
Vizsgáljuk most a feladat szerinti elrendezést!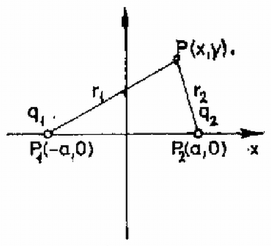

1. ábra

Tegyük fel, hogy ezeket a töltéseket is vákuum veszi körül. Jelöljük a

P_{1}

és

P_{2}

pontok közti távolságot

2 a

-val és válasszuk úgy derékszögű koordináta-rendszerünket, hogy

P_{1}

koordinátái legyenek

(- a,0,0)

P_{2}

-é pedig

(a,0,0)

. Mivel az

x

tengely körül megforgatva a rendszert, az elrendezés mindig önmagába megy át, ezért elegendő az

x - y

sík szemléltetése, az

y - z

síkban minden felület metszete kör. Egy

P (x, y)

pontban a potenciál (l. az 1. ábrát):

\begin{matrix} U (x, y) = \frac{1}{4 π ε_{0}} \cdot \frac{q_{1}}{r_{1}} + \frac{1}{4 π ε_{0}} \cdot \frac{q_{2}}{r_{2}} = \frac{1}{4 π ε_{0}} (\frac{q_{1}}{\sqrt[]{{(x + a)}^{2} + y^{2}}} + \frac{q_{2}}{\sqrt[]{{(x - a)}^{2} + y^{2}}}) . \end{matrix}

Vezessük be a következő jelölést:

q_{1} = q; q_{2} = k q

. Ekkor az ekvipotenciális felület

x - y

síkkal való metszetének egyenlete:

\begin{matrix} \frac{1}{\sqrt[]{{(x + a)}^{2} + y^{2}}} + \frac{k}{\sqrt[]{{(x - a)}^{2} + y^{2}}} = C, \end{matrix}

(1)

ahol

C

állandó, arányos az

U

potenciállal.
Vizsgáljuk meg, hogy milyen felületeket kapunk néhány speciális esetben.
a) Legyen

x - a ≪ a

y ≪ a

, vagyis vizsgáljuk az ekvipotenciális felületeket a

P_{2}

pont közelében. Ez azt jelenti, hogy

x

értéke közelítőleg

a

x + a

értéke közelítőleg

2 a

y

pedig

2 a

mellett is elhanyagolhatóan kicsiny. Így az (1) egyenlet így írható:

\begin{matrix} \frac{1}{2 a} + \frac{k}{\sqrt[]{{(x - a)}^{2} + y^{2}}} = C . \end{matrix}

(2)

Mivel a bal oldal első tagja a feltételeink miatt jóval kisebb a második tagnál, ezért (2) helyett

\begin{matrix} \frac{k}{\sqrt[]{{(x - a)}^{2} + y^{2}}} = C \end{matrix}

írható, ami az

\begin{matrix} {(x - a)}^{2} + y^{2} = állandó \end{matrix}

alakra hozható. Ez egy kör egyenlete, amelynek a középpontja a

P_{2}

pont. Így biztosan vannak olyan ekvipotenciális felületek a

P_{2}

pont körül (és hasonló módon belátható, hogy a

P_{1}

pont körül is), amelyeknek az alakja gömb, mintha a másik töltés ott sem lenne, azonban ezen felületek sugara jóval kisebb, mint

a

. Ez érthető is, hiszen egy ponttöltéshez nagyon közel a tér többi töltésének hatása elhanyagolhatóan kicsi a ponttöltés saját teréhez képest (a Coulomb-erő a távolság négyzetével fordítottan arányos).
b) Legyen

k < 0

, azaz a két töltés legyen ellenkező előjelű. Keressük a nulla potenciálhoz tartozó ekvipotenciális felületet! (1) most a következőképpen alakul:

\begin{matrix} \frac{1}{\sqrt[]{{(x + a)}^{2} + y^{2}}} = - \frac{k}{\sqrt[]{{(x - y)}^{2} + y^{2}}} . \end{matrix}

(

k

negatív, így mindkét oldal pozitív.) Az egyenlet reciprokát véve, négyzetre emelés és rendezés után kapjuk, hogy

\begin{matrix} k^{2} [{(x + a)}^{2} + y^{2}] = {(x - a)}^{2} + y^{2}, \end{matrix}

(3)

ami a következő alakra hozható:

\begin{matrix} {(x + a \frac{k^{2} + 1}{k^{2} - 1})}^{2} + y^{2} = {(\frac{2 k a}{k^{2} - 1})}^{2}, \end{matrix}

ami egy olyan kör egyenlete (ha

k \neq - 1

), amelynek sugara

R_{0} = - \frac{2 k a}{k^{2} - 1}

, középpontja pedig az

x

tengelyen, az

x_{0} = - a \frac{k^{2} + 1}{k^{2} - 1}

koordinátájú pontban van. Ezt a kört láthatjuk a 2. ábrán a

k = - 2

esetben

[x_{0} = - (5 / 3) a, R_{0} = (4 / 3) a]

k > - 1

esetén a kör (gömb) a

P_{2}

pontot, vagyis a kisebb abszolút értékű töltést veszi körül.

2. ábra

k = - 1

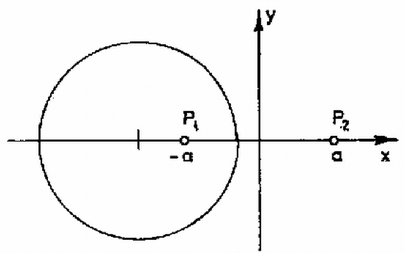, akkor a (3) egyenletet nem szabad

k^{2} - 1

-gyel elosztani, helyette (3)-ból

\begin{matrix} 4 a x = 0, \end{matrix}

azaz

x = 0

adódik. Ez éppen az

x - z

sík egyenlete. Az ekvipotenciális felület ebben az esetben (a két töltés azonos nagyságú, de ellenkező előjelű) tehát a

P_{1} P_{2}

szakaszt felező, a szakaszra merőleges sík.
c) Legyen

k \neq - 1

. Keressük azt az ekvipotenciális felületet, amely jóval messzebb van a töltésektől, mint azok egymástól (

x, y ≫ a

)! Ekkor az (1) egyenletben

x

mellett

a

elhanyagolható:

\begin{matrix} \frac{1}{\sqrt[]{x^{2} + y^{2}}} + \frac{k}{\sqrt[]{x^{2} + y^{2}}} = C, \end{matrix}

vagyis

\begin{matrix} x^{2} + y^{2} = {(\frac{1 + k}{C})}^{2}, \end{matrix}

ami egy olyan kör egyenlete, amelynek középpontja koordináta-rendszerünk középpontja, azaz a

P_{1} P_{2}

szakasz felezőpontja. Így, ha messze vagyunk a töltésektől, a tér már csak az eredő töltést veszi figyelembe, a töltések eloszlásának nincsen hatása az ekvipotenciális felületekre; az ekvipotenciális felületek a töltésektől messze gömbfelületek.
Mivel az (1) egyenletet általánosan megoldani nem tudjuk, meg kell elégednünk az eddig tárgyalt speciális esetekkel, ezek segítségével azonban közelítőleg mégis meg tudjuk rajzolni az ekvipotenciális felületeket. A 3., 4. és 5. ábrán szaggatott vonallal rajzoltuk ekvipotenciális felületek azon metszésvonalait, amelyeket a megoldásban nem számoltunk ki, amelyek alakját "érzés'' alapján rajzoltuk meg. Segített a rajzolásban az is, hogy az ekvipotenciális felületet mindig merőlegesen metszi a térerősség iránya, azaz az erővonal.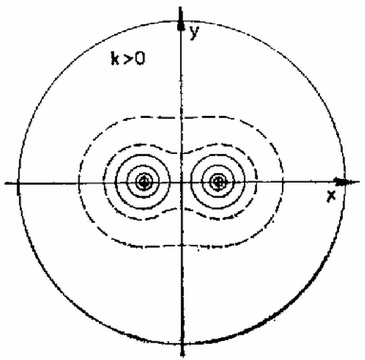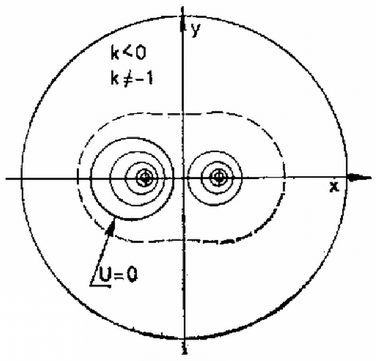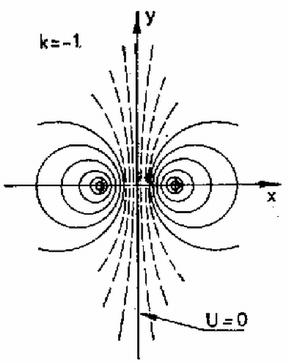

3. ábra

4. ábra

5. ábra

A fentiekből az is egyértelműen látható, hogy minden esetben létezik ekvipotenciális felület, sőt az is igaz, hogy a

P_{1}

és

P_{2}

pontok kivételével a tér tetszőleges pontjára illeszkedik ekvipotenciális felület.

Drávucz Katalin (Szolnok, Verseghy F. Gimn., IV. o. t.)
dolgozata alapján