| Feladat: | 1726. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Csillag Péter , Erdős László , Fodor Gyula , Furó István , Kristóf Péter | ||
| Füzet: | 1982/február, 89 - 92. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Erők forgatónyomatéka, Párhuzamos erők eredője, Hajlítás, Szakítószilárdság, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1981/október: 1726. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.A rúd bármely pontjában ható erő csak a rögzített vég és az erő támadáspontja között elhelyezkedő rúddarabra hat (ez a rúddarab deformálódik), a támadáspontján kívüleső rúddarab ,,nem érzi'' az erő jelenlétét (ez a rész nem deformálódik). Hogy a rögzítési ponttól távolságra levő pontban, eltörik-e a rúd vagy sem, az attól függ, hogy a ponton kívül (a rögzítési ponttól távolabb) ható erők által a pontra ható forgatónyomaték abszolút értéke kisebb vagy nagyobb-e -nél (1. ábra). Ha kisebb, úgy nem törik el az pontban a rúd, ha nagyobb, akkor eltörik. (Nem csak a végpontbeli törést kell vizsgálnunk.) Vizsgáljuk meg, milyen feltételt rovunk ki így -re. Ha akkor mindhárom erő támadáspontján belül vagyunk, tehát mindhárom erő forgatónyomatékát figyelembe kell vennünk. 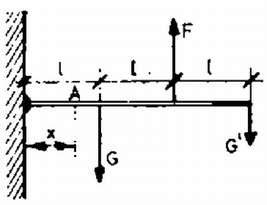
Ha , azaz , az egyenlőtlenségnek maximális értékénél is fenn kell állnia, azaz -nél is. Így , azaz . A másik oldal: Tehát Az (1) egyenlőtlenség másik oldalát vizsgáljuk meg ezután. Ezekből következik, hogy esetén a egyenlőtlenségnek, esetén pedig a egyenlőtlenségnek kell teljesülnie. A két feltételrendszert összeolvasztva: Ábrázoljuk grafikusan (l. a 2. ábrát) a feltételeket, a besatírozott rész jelenti adott és mellett lehetséges értékeit. 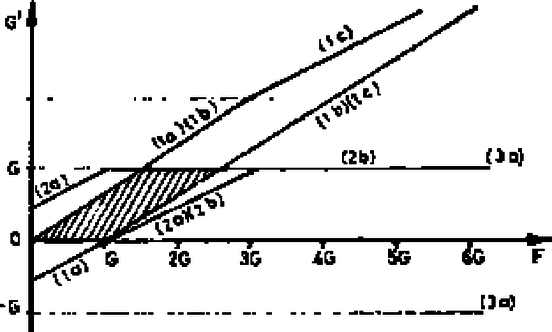 2. ábra Mivel a rúdra akasztott súlyról volt szó, így pozitív értékeit (-vel egyirányú) vesszük csak figyelembe. Ezek alapján a feltételek: |