Kezdőlap


Feladat:	1714. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hatt János , Simon László
Füzet:	1981/december, 231 - 232. oldal		PDF \| MathML
Témakör(ök):	Impulzusváltozás törvénye (Pontrendszer impulzusa), Pontrendszerek mozgásegyenletei, Nyújtás, összenyomás, Csúszó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1981/május: 1714. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tegyük fel, hogy $F$ támadáspontja a rúd végében van. Osszuk fel a rudat $n$ egyenlő részre. A különböző helyen levő rúddarabokban különböző nagyságú erők hatnak. Ha a felosztás elég finom, közelítőleg állandónak vehetjük egy kis darab bármely keresztmetszetében a ható erőt. Az $n$ -edik darabra ható $F_{n}$ erő egyrészt ellensúlyozza az $(m g / n)$ $μ$ súrlódási erőt, másrészt $a$ gyorsulással mozgatja az $m / n$ tömegű rúddarabot:

\begin{matrix} F_{n} = (m / n) (a + μ g) . \end{matrix}

(1)

n

-edik darab megnyúlása

\begin{matrix} Δ l_{n} = (E / A) (L / n) \cdot F_{n} . \end{matrix}

(n - 1)

-edik keresztmetszetben ható erő a mögötte levő két darabot gyorsítja: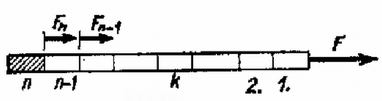

\begin{matrix} F_{n - 1} = 2 F_{n}, \end{matrix}

míg a

k

-adik rész

(k + 1)

részt gyorsít és így

\begin{matrix} F_{n - k} = (k + 1) F_{n} . \end{matrix}

1. ábra

(n - 1)

-edik darab megnyúlása:

\begin{matrix} Δ l_{n - 1} = (E / A) (L / n) F_{n - 1}, \end{matrix}

míg a

k

-adik rész megnyúlása:

\begin{matrix} Δ l_{n - k} = (E / A) (L / n) F_{n - k} . \end{matrix}

A teljes megnyúlás az egyes részek megnyúlásainak összege.

\begin{matrix} Δ l = \sum_{i = 1}^{n} Δ l_{i} = \frac{E m L (a + μ g)}{2 A} . \end{matrix}

(2)

Itt felhasználtuk, hogy

(n + 1) / n \approx 1

, ha

n

elég nagy.
Ha a rudat gyorsító

F

erőt ismerjük, akkor a gyorsulás:

\begin{matrix} a = \frac{F - m g μ}{m}, \end{matrix}

(3)

ezzel

\begin{matrix} Δ l = \frac{E L F}{2 R^{2} π} . \end{matrix}

(4)

Simon László (Bp, Madách I. Gimn., III. o. t.)

Megjegyzés. Nem volt kikötve, hogy a rudat mozgató erő hol hat, és mint látni fogjuk, ettől lényegesen függ az eredmény.
Tegyük fel, hogy a rúd végétől

x

távolságra van a támadáspont. A támadáspont előtt levő rész megnyúlása (2) alapján (

L \to x

helyettesítéssel és az irány miatt negatív előjellel):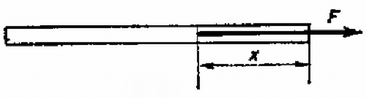

\begin{matrix} Δ l_{1} = \frac{E m x (a + μ g)}{2 A} . \end{matrix}

2. ábra

A támadáspont mögötti rész megnyúlása pedig

\begin{matrix} Δ l_{2} = \frac{E m (L - x) (a + μ g)}{2 A} . \end{matrix}

(3) felhasználásával

\begin{matrix} Δ l = A l_{1} + A l_{2} = \frac{E m F (L - 2 x)}{2 A} . \end{matrix}

Hatt János (Mosonmagyaróvár,Kossuth L. Gimn., III. o. t.)