Kezdőlap


Feladat:	1709. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kovács Attila , Oszlányi Gábor
Füzet:	1981/december, 226 - 228. oldal		PDF \| MathML
Témakör(ök):	Forgási energia, Gördülés vízszintes felületen, Merev testek ütközése, Csúszó súrlódás, Tökéletesen rugalmas ütközések, Impulzusváltozás törvénye (Pontrendszer impulzusa), Feladat
Hivatkozás(ok):	Feladatok: 1981/április: 1709. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A pattogás során a golyó egyre nagyobb vízszintes sebességösszetevőhöz jut, miközben a forgó mozgás kerületi sebessége csökken. Ha a két sebesség kiegyenlítődik, vagyis $v_{v} = r ω$ , akkor ettől a pillanattól kezdve a golyó elméletileg a végtelenségig fog állandó vízszintes sebességöesszetevővel és állandó szögsebességgel forogva pattogni. A mozgás függőleges összetevője periodikus: a $h$ magasságból szabadon eső golyó tökéletesen rugalmasan ütközve visszapattan és $h$ magasságig emelkedik, majd újra visszaesik stb.
Vizsgáljuk az $n$ -edik ütközést! A golyó $v_{f} = - \sqrt[]{2 g h} = - v_{0}$ lefelé mutató függőleges sebességösszetevővel érkezik a lapra, és $v'_{f} = v_{0}$ felfelé mutató függőleges sebességgel hagyja el azt, az ütközés során a függőleges impulzus-változás 2 $m v_{0}$ . Erről tudjuk, hogy

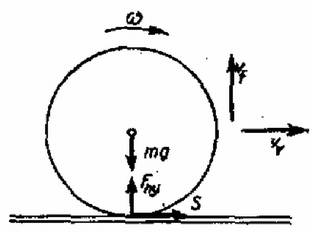\begin{matrix} 2 m v_{0} = ({\bar{F}}_{n y} - g m) Δ t \approx {\bar{F}}_{n y} Δ t \end{matrix}

(1)

1. ábra

(

{\bar{F}}_{n y}

a lap és a golyó között fellépő nyomóerőnek az ütközés

Δ t

idejére vett átlaga,

\begin{matrix} {\bar{F}}_{n y} = \frac{1}{Δ t} \int_{0}^{Δ t} F_{n y} (t) d t; \end{matrix}

mivel az ütközés nagyon rövid ideig tart, az impulzusváltozás pedig véges nagyságú,

F_{n y}

-nak nagy értéknek kell lennie, ezért mellette

m g

elhanyagolható.) A vízszintes impulzusváltozást a súrlódási erő hozza létre, feltéve hogy a golyó az egész

Δ t

idő alatt "köszörül''

\bar{S} = μ F_{n y}

és így

\begin{matrix} m (v_{v, n} - v_{v, n - 1}) = μ \cdot {\bar{F}}_{n y} \cdot Δ t = μ \cdot 2 m v_{0}, \end{matrix}

(2)

tehát

\begin{matrix} v_{v, n} = v_{v, n - 1} + 2 μ v_{0} . \end{matrix}

(3)

A súrlódási erő forgatónyomatéka a forgást fékezi:

\begin{matrix} Θ (ω_{n} - ω_{n - 1}) = - r μ F_{n y} Δ t = - r \cdot 2 μ m v_{0}, \end{matrix}

(4)

így

\begin{matrix} ω_{n} = ω_{n - 1} - \frac{5 μ v_{0}}{r} . \end{matrix}

(5)

Itt felhasználtuk, hogy

Θ

a tömör gömbre

2 m r^{2} / 5

.
A (3) és (5) összefüggésekből a golyó

n

-edik ütközés utáni vízszintes sebessége és szögsebessége

\begin{matrix} v_{v, n} = n \cdot 2 μ v_{0}, \end{matrix}

(6)

\begin{matrix} ω = ω_{0} - n \frac{5 μ v_{0}}{r} . \end{matrix}

(7)

Mindez akkor igaz, ha a golyó az

n

-edik ütközés teljes időtartama alatt köszörült, azaz

\begin{matrix} v_{v, n} ≦ ω_{n} r, \end{matrix}

(8)

vagyis

\begin{matrix} n \cdot 7 \cdot μ \cdot v_{0} ≦ ω_{0} r . \end{matrix}

(9)

Mi történik, ha a (9) egyenlőtlenség

n - 1

-re még igaz, de

n

-re már nem áll fenn (

n

lehet

1

is)? Ekkor az

n

-edik ütközés alatt, abban a pillanatban amikor vízszintes sebesség és a forgásból adódó kerületi sebesség azonossá válik, megszűnik a köszörülés, megszűnik a súrlódás, a golyónak sem vízszintes sebességösszetevője, sem a szögsebessége nem változik tovább. Nyilván a további pattogások során sem változnak ezek a mennyiségek. Legyen az

F_{n y}

erő átlaga arra a

Δ t^{*}

időre, amíg az n-edik ütközés során a köszörülés tart,

F_{n y}^{*}

és legyen a beálló szögsebesség és vízszintes sebességössztevő rendre

ω^{*}

és

v_{r}^{*}

! Ekkor

\begin{matrix} m (v_{r}^{*} - v_{v, n - 1}) = μ F_{n y}^{*} Δ t^{*}, \end{matrix}

(10)

\begin{matrix} (2 / 5) m r^{2} (ω^{*} - ω_{n - 1}) = - μ F_{n y}^{*} Δ t^{*}, \end{matrix}

(11)

\begin{matrix} v_{v}^{*} = ω^{*} \cdot r . \end{matrix}

(12)

A (10), (11) és (12) egyenletrendszer megoldása (6) és (7) felhasználásával:

\begin{matrix} v_{v}^{*} = (2 / 7) ω_{0} \cdot r, \end{matrix}

(13)

\begin{matrix} ω^{*} = (2 / 7) ω_{0} . \end{matrix}

(14)

Tehát a golyó vízszintes irányú sebessége minden ütközés során

2 μ \sqrt[]{2 g h}

értékkel nő, míg a szögsebessége

5 μ \sqrt[]{2 g h} / r

értékkel csökken. Ez egészen addig tart, amíg a sebesség el nem éri a

2 ω_{0} r / 7

, a szögsebesség pedig a

2 ω_{0} / 7

értéket, az ezután következő pattanások során már sem a vízszintes sebesség, sem pedig a szögsebesség nem változik. A 2. ábra a golyó

v_{f}

függőleges,

v_{v}

vízszintes sebességét, valamint az

ω

szögsebességét ábrázolja az idő függvényében.

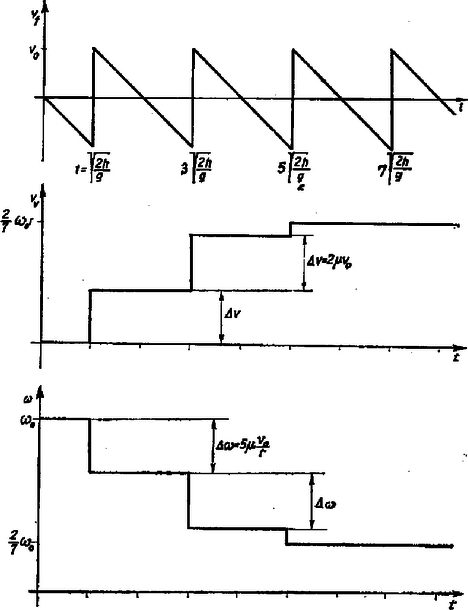2. ábra

Kovács Attila (Kalocsa, I. István Gimn., III. o. t.)
és Oszlányi Gábor (Miskolc, Földes F. Gimn., III. o. t.)
dolgozata alapján