| Feladat: | 1701. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Boszágh Péter , Horváth István , Kaptás Dénes , Kiss Péter , Lóczi Géza , Oszlányi Gábor , Sczigel Gábor , Szállási Zoltán | ||
| Füzet: | 1981/november, 175 - 176. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Pontrendszerek mozgásegyenletei, Súrlódás, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1981/március: 1701. fizika feladat | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladat teljes megoldása nagyon hosszadalmas, ezért csak a megoldás vázlatát fogjuk ismertetni. Elsősorban nem a gyorsulások értékének megadására, hanem a feladat áttekinthető tárgyalására fogunk törekedni. Legyen a hasáb lejtő irányú gyorsulása ; a hasáb vízszintes lapján levő test gyorsulásának vízszintes összetevője , a függőleges fal mellett lógó test függőleges gyorsulása . 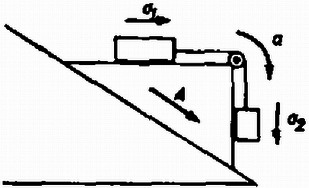 1. ábra A gyorsulások irányítását az 1. ábra mutatja. Legyen az tömegű testeknek a lejtőhöz viszonyított gyorsulása . Ekkor A vízszintes lapon levő tömeg függőleges gyorsulása , a lelógó test gyorsulásának vízszintes összetevője . ha és így a test a hasáb függőleges falához ér, illetve , ha . Ez utóbbi esetben meggondolásaink csak az indulás pillanatára érvényesek, később a fonál nem függőleges helyzetű. Írjuk föl a három testre a mozgásegyenleteket, feltéve hogy . A 2. ábra a hasábra ható erőket mutatja, a súrlódási erők irányítása jobbra mozgó hasáb és tömegek esetének felel meg.  2. ábra A mozgásegyenletet a vízszintes és függőleges komponensekre írjuk föl; a hasáb mozgásegyenlete: A 3. ábra a két tömegű testre ható erőket mutatja. 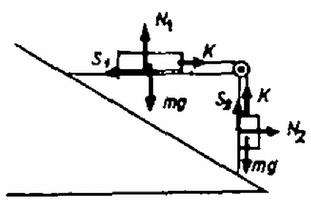 3. ábra Ismét vízszintes és függőleges komponensekben dolgozva, a mozgásegyenletek a következők: Vizsgáljuk meg, hogy és függvényében milyen esetek lehetségesek! Az eredményeket a 4. ábrán foglaltuk össze. 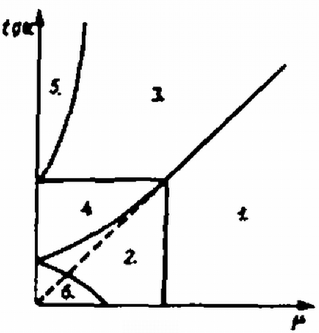 4. ábra 1. és . Ekkor a lelógó test nem nyomódik a hasábhoz, és így . A (3)-(8) egyenletrendszert is felhasználva a tapadás , ill. feltételéből a és feltételek adódnak. 2. és . Ekkor is , , mivel a test csúszik. Az feltételből adódik, pedig akkor teljesül, ha két, -től és a tömegektől függő érték közé esik (l. a ábrát). 3. és . Ekkor , amit felhasználva a nyilvánvaló eredmény adódik. Ez akkor pozitív, ha . A tapadás miatt és . Ennek a két feltételnek az együttes kezelése nagyon bonyolult lenne, mivel és nem fejezhető ki külön-külön az egyenletrendszerből. Meghatározható viszont és kihasználva, hogy a megcsúszás határhelyzeteiben és egy irányba mutat, írhatjuk a két feltétel helyett az egyenlőtlenséget. Ennek taglalásából és adódik, ahol az függvény az egyenletrendszer megoldásából meghatározható. 4. és . Ebben az esetben valamennyi felületnél csúszás lép fel, a relatív elmozdulás iránya megegyezik az ábrák rajzolásakor feltételezettel. Így a (3)-(8) egyenletekhez az , és az egyenletek járulnak, az egyenletrendszerből és meghatározható. Az feltevésből , az , feltevésből 5. , . Ekkor és iránya a berajzolttal ellentétes, így , , és . Ez az eset meredek és csúszós lejtő esetén áll fenn, -ból , -ból -re -tól függő felső határ adódik. 6. és . Egyenleteink ekkor csak az elengedés pillanatában érvényesek, hosszú idő után ugyanis a függőleges fal mellett lógó kötél nem függőleges. , és így már az induláskor is fennáll, nem igaz azonban a (8) egyenlet, hiszen a függőleges kötélen lógó tömeg induláskor vízszintesen nem gyorsul. A csúszás miatt és . Ezeket az egyenleteket (3)-(7)-tel kombinálva a gyorsulások meghatározhatók. Az feltétel akkor áll fenn, ha Kaptás Dénes (Nagykőrös, Arany J. Gimn. IV. o. t.) dolgozata alapján |