Kezdőlap


Feladat:	1700. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Mandula Gábor
Füzet:	1981/november, 173 - 174. oldal		PDF \| MathML
Témakör(ök):	Egyenletes mozgás (Tömegpont mozgásegyenelete), Egyenletesen változó mozgás (Tömegpont mozgásegyenelete), Feladat
Hivatkozás(ok):	Feladatok: 1981/március: 1700. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vizsgáljuk azt az esetet, amikor a láda $a$ gyorsulással mozog a lejtőn felfelé, ahol $a \geq 0$ . Ekkor a ládára ható erőket az ábra szemlélteti.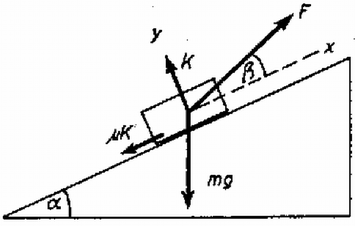

Legyen a láda tömege

m

, a húzóerő nagysága

F

, ennek lejtő irányú komponense

F_{x}

, a lejtőre merőleges komponense

F_{y}

, az

F

erő lejtővel bezárt szöge

β

(l. az ábrát). Írjuk fel a ládára ható lejtő irányú, illetve lejtőre merőleges erők egyensúlyát:

\begin{matrix} m g sin α + μ K + m a = F_{x}, & (1) \\ K + F_{y} = m g cos α, & (2) \end{matrix}

ahol

K

a ládára ható nyomóerő. A (2) egyenletből adódik a

\begin{matrix} K = m g cos α - F_{y} \geq 0 \end{matrix}

(3)

megkötés. A feladatunk

\begin{matrix} F = \sqrt[]{F_{x}^{2} + F_{y}^{2}} \end{matrix}

minimalizálása. (1), (2)-ből

F_{x}

-re és

F_{y}

-ra kapjuk:

\begin{matrix} m g sin α + μ (m g cos α - F_{y}) + m a = F_{x} . \end{matrix}

(4)

F

akkor minimális, ha négyzete minimális.

\begin{matrix} F^{2} = {[m g sin α + μ (m g cos α - F_{y}) + m a]}^{2} + F_{y}^{2} = \\ = F_{y}^{2} (1 + μ^{2}) - F_{y} (2 μ m g sin α + 2 μ^{2} m g cos α + 2 μ m a) + m^{2} g^{2} sin^{2} α + \\ + μ^{2} m^{2} g^{2} cos^{2} α + m^{2} a^{2} + 2 μ m^{2} g^{2} sin α cos α + 2 m^{2} g a \end{matrix}