Feladat:	1680. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ábrahám Csongor ,  Benedek Tibor ,  Kesztyüs Gábor ,  Kuna János ,  Lóczi Géza ,  Mogyorósi András ,  Szállási Zoltán ,  Varga Kálmán
Füzet:	1981/április, 186 - 188. oldal		PDF  |  MathML
Témakör(ök):	Merev testek ütközése, Fizikai inga, Forgási energia, Merev test impulzusnyomatéka (perdülete), Feladat
Hivatkozás(ok):	Feladatok: 1980/december: 1680. fizika feladat

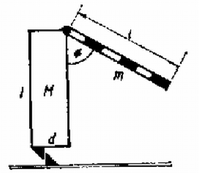
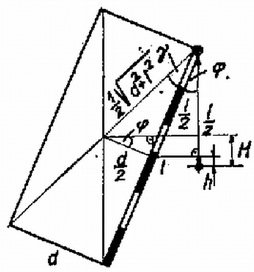
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A csapó léc elengedése után helyzeti energiája forgási energiává alakul át. A léc tömegközéppontjának süllyedése: $\left(l/2\right)-\left(l/2\right)\text{cos}\alpha$ (l. az ábrát). Felírhatjuk tehát, hogy $\begin{array}{c}{\displaystyle mg\left(l/2\right)\left(1-\text{cos}\alpha \right)=\left(1/2\right){\Theta }_m{\omega }_1^2\mathrm{,}}\end{array}$ ahol ${\Theta }_m=\left(1/3\right)m{l}^2=3\cdot {10}^{-3}{\text{<span style="font-weight: normal;font-style: normal;">kgm</span>}}^2$ a léc tehetetlenségi nyomatéka, és ${\omega }_1$ a szögsebessége az ütközés pillanatában. A fentiekből megkapjuk ${\omega }_1$-et: $\begin{array}{c}{\displaystyle {\omega }_1=\sqrt[]{\frac{3g\left(1-\text{cos}\alpha \right)}{l}}=7\frac{1}{\text{<span style="font-weight: normal;font-style: normal;">s</span>}}\mathrm{.}}\end{array}$ Most számítsuk ki a téglalap alakú lemeznek a felfüggesztési pontra vonatkoztatott tehetetlenségi nyomatékát. A függvénytáblázatban megtalálható a tömegközéppontra vonatkozó tehetetlenségi nyomaték: $\left(1/12\right)M\left(l^2+d^2\right)$. A tömegközéppont és a felfüggesztés távolsága $\sqrt[]{d^2+l^2}/2$. A Steiner-tételt használva: $\begin{array}{c}{\displaystyle {\Theta }_m=\frac{1}{12}M\left(l^2+d^2\right)+M\frac{d^2+l^2}{4}=\frac{1}{3}M\left(d^2+l^2\right)=1\mathrm{,}66\cdot {10}^{-2}{\text{<span style="font-weight: normal;font-style: normal;">kgm</span>}}^2\mathrm{.}}\end{array}$ Vizsgáljuk először az a) esetet, amikor az ütközés teljesen rugalmas. Ekkor felírhatjuk az ütközésre a forgásmennyiség és az energia megmaradására vonatkozó egyenleteket. Jelölje ${\omega }_m$, ill. ${\omega }_M$ a testek ütközés utáni szögsebességét. Így ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\omega }_1{\Theta }_m={\omega }_m{\Theta }_m+{\omega }_M{\Theta }_M\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(1/2\right){\Theta }_m{\omega }_1^2=\left(1/2\right){\Theta }_m{\omega }_m^2+\left(1/2\right){\Theta }_M{\omega }_M^2\mathrm{.}}\hfill \end{array}}$ Az egyenletrendszert megoldva kapjuk, hogy ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\omega }_m=\frac{{\omega }_1\left({\Theta }_m-{\Theta }_M\right)}{{\Theta }_m+{\Theta }_M}=-4\mathrm{,}86\frac{1}{\text{<span style="font-weight: normal;font-style: normal;">S</span>}};}\hfill \\ \hfill {\displaystyle {\omega }_M=\frac{2{\Theta }_m{\omega }_1}{{\Theta }_m+{\Theta }_M}=2\mathrm{,}14\frac{1}{\text{<span style="font-weight: normal;font-style: normal;">S</span>}}\mathrm{.}}\hfill \end{array}}$ Ismét az energiamegmaradást felhasználva, kapjuk a léc, illetve a lemez emelkedési magasságát: $\begin{array}{c}{\displaystyle mgh=\left(1/2\right){\Theta }_m{\omega }_m^2\mathrm{,}MgH=\left(1/2\right){\Theta }_M{\omega }_M^2\mathrm{,}}\end{array}$ amiből $\begin{array}{c}{\displaystyle h=\frac{l^2}{6g}{\omega }_m^2=3\mathrm{,}61\cdot {10}^{-2}\text{<span style="font-weight: normal;font-style: normal;">m</span>};H=\frac{l^2+d^2}{6g}{\omega }_m^2=\mathrm{7,8}\cdot {10}^{-3}\text{<span style="font-weight: normal;font-style: normal;">m</span>}\mathrm{.}}\end{array}$ b) Most vizsgáljuk a rugalmatlan ütközés esetét. Jelöljük ${\omega }_2$ vel az ütközés utáni közös szögsebességet. Most csak a forgásmennyiség megmaradására vonatkozó egyenletet írhatjuk fel: $\begin{array}{c}{\displaystyle {\omega }_1{\Theta }_m={\omega }_2\left({\Theta }_m+{\Theta }_M\right)\mathrm{,}{\omega }_2=\frac{{\omega }_1{\Theta }_m}{{\Theta }_m+{\Theta }_M}=1\mathrm{,}0721/\text{<span style="font-weight: normal;font-style: normal;">s</span>}\mathrm{.}}\end{array}$ Az ütközés utáni pillanatban a mozgási energia $E=\left(1/2\right)\left({\Theta }_m+{\Theta }_M\right){\omega }_2^2=1\mathrm{,}13\cdot {10}^{-2}\text{<span style="font-weight: normal;font-style: normal;">J</span>}\mathrm{.}$ Most vizsgáljuk meg, hogy együtt mozog-e a két test az ütközés után. Nézzük meg, mekkora lenne a testek szöggyorsulása $\phi$ szögű elfordulás után, ha külön-külön mozognának! A pálcára ható forgatónyomaték: $mg\left(l/2\right)\text{sin}\phi$ (l. az ábrát). A szöggyorsulása: $\begin{array}{c}{\displaystyle {\beta }_m=\frac{mg\left(l/2\right)\text{sin}\phi }{{\Theta }_m}=\frac{3g\text{sin}\phi }{2l}\mathrm{.}}\end{array}$ A lemezre ható forgónyomaték $Mg\frac{\sqrt[]{l^2+d^2}}{2}\text{sin}\left(\phi +y\right)\mathrm{,}$ valamint $\text{sin}y=\frac{d}{\sqrt[]{l^2+d^2}}$ és $\text{cos}y=\frac{l}{\sqrt[]{l^2+d^2}}\mathrm{.}$ Tehát a szöggyorsulás: $\begin{array}{c}{\displaystyle {\beta }_M=\frac{Mg\left(\sqrt[]{l^2+d^2}/2\right)\text{sin}\left(\phi +y\right)}{{\Theta }_M}=\frac{3g\left(l\text{sin}\phi +d\text{cos}\phi \right)}{2\left(l^2+d^2\right)}\mathrm{.}}\end{array}$ Osszuk el őket egymással, hogy összehasonlítsuk őket. Az egyszerűsítések után: $\begin{array}{c}{\displaystyle \frac{{\beta }_M}{{\beta }_m}=\frac{l^2+dl\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\phi }{l^2+d^2}\mathrm{.}}\end{array}$ Látható, hogy ez nagyobb egynél, ha $l\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\phi >d$, azaz $\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\phi >\text{<span style="font-weight: normal;font-style: normal;">tg</span>}y$. Tehát ${\beta }_M>{\beta }_m$, ha $\phi <{90}^{\circ }-y$, azaz $\phi <{71}^{\circ }34\text{'}$. Ha a két test együtt indul az alsó helyzetből, akkor mindaddig egymáshoz nyomódnak, amíg a pálca előbb kiszámított lassulása kisebb a lemezénél, tehát ${71}^{\circ }34\text{'}$ kitérésig együtt mozognak. A pálcát ${60}^{\circ }$-os szögből indítottuk, így nem lehetséges, hogy a két test az ütközés után ennél jobban kitérjen, tehát a rugalmatlan ütközés után a maximális kitérésig együtt fognak mozogni. $\phi$ szögű kitérés esetén a pálca tömegközéppontjának emelkedése $h=\left(l/2\right)\left(1-\text{cos}\phi \right)$. A lemezé pedig $H=h+\left(d/2\right)\text{sin}\phi$. A két egyenletből $\phi$-t kiküszöbölve kapjuk: $\begin{array}{c}{\displaystyle H=h+d\sqrt[]{\left(h/l\right)-\left(h^2/l^2\right)}\mathrm{.}}\end{array}$ Az energiamegmaradás törvénye szerint $mgh+MgH=E$. E két egyenletből álló egyenletrendszert megoldva $h$-ra egy másodfokú egyenletet kapunk: $\begin{array}{c}{\displaystyle h^2\left[g^2{\left(m+M\right)}^2+M^2{g}^2{d}^2{l}^{-2}\right]-h\left[2Eg\left(m+M\right)+M^2{g}^2{d}^2{l}^{-1}\right]+E^2=0.}\end{array}$ Megoldva és adatainkat behelyettesítve kapjuk, hogy $\begin{array}{c}{\displaystyle h=1\mathrm{,}37\cdot {10}^{-4}\text{<span style="font-weight: normal;font-style: normal;">m</span>}\text{<span style="font-weight: normal;font-style: normal;">és</span>}H=2\mathrm{,}28\cdot {10}^{-3}\text{<span style="font-weight: normal;font-style: normal;">m</span>}\mathrm{.}}\end{array}$  Szállási Zoltán (Esztergom, Dobó K. Gimn., III. o. t.)  dolgozata alapján.