Kezdőlap


Feladat:	1679. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Fehér Péter , Kuna János
Füzet:	1981/május, 234 - 238. oldal		PDF \| MathML
Témakör(ök):	Körmozgás (Tömegpont mozgásegyenlete), Newton-féle gravitációs erő, Impulzusváltozás törvénye (Pontrendszer impulzusa), Kepler III. törvénye, Kepler I. törvénye, Feladat
Hivatkozás(ok):	Feladatok: 1980/december: 1679. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A pálya mentén kitett test és az űrhajó mozgása jó közelítéssel felfogható úgy, hogy mindketten azonos pályán mozognak, és erre a mozgásukra szuperponálódva a kölcsönös vonzás hatására egymás felé esnek. Célszerű a relatív mozgásukat a közös súlyponthoz rögzített koordináta-rendszerből vizsgálni. Ebben a koordináta-rendszerben a $M$ tömegű űrhajó nyugvónak tekinthető, hiszen az űrhajó sebessége $m / M$ -szer kisebb, mint a $m$ tömegű kitett tárgyé. Feladatunk tehát az, hogy meghatározzuk, mennyi idő alatt esik rá az $R = 19$ m sugarú űrhajóra a falától $h = 3$ m távolságra levő tárgy. A tárgy gyorsulása az esés közben állandóan változik, célszerű ezért a becsapódás helyét a következő módon meghatározni. Az energiamegmaradás szerint a tárgy sebessége és a faltól való $x$ távolság között az

\begin{matrix} \frac{1}{2} m v^{2} = γ m M (\frac{1}{R + x} - \frac{1}{R + h}) \end{matrix}

(1)

összefüggés áll fenn, azaz

\begin{matrix} v = \sqrt[]{2 γ M (\frac{1}{R + x} - \frac{1}{R + h})} . \end{matrix}

(2)

Ezt a sebességet állandónak véve, amíg az

x

(x - Δ x)

-re csökken, azt találjuk, hogy a faltól

x

távolságra levő kicsiny

Δ x

hosszúságú szakasz megtételéhez

\begin{matrix} Δ t = \frac{Δ x}{{[2 M γ (\frac{1}{R + x} - \frac{1}{R + h})]}^{1 / 2}} \end{matrix}

(3)

idő szükséges.
Bontsuk fel a

(0, h)

intervallumot az

x_{i}

osztópontok segítségével kicsiny,

Δ x_{i}

hosszúságú részekre

(i = 1,2, ..., n)

, így (3) alapján azt kapjuk, hogy a teljes

h

távolság befutásához szükséges idő közelítőleg

\begin{matrix} \sum_{i = 1}^{n} \frac{Δ x_{i}}{{[2 M γ (\frac{1}{R + x_{i}} - \frac{1}{R + h})]}^{1 / 2}} . \end{matrix}

(0, h)

intervallum felosztását minden határon túl finomítva, a fenti összeg határértéke az

\begin{matrix} \int_{0}^{h} \frac{d x}{{(2 γ M)}^{1 / 2} {(\frac{1}{R + x} - \frac{1}{R + h})}^{1 / 2}} \end{matrix}

(4)

integrál, ami pontosan megadja a

h

távolság megtételéhez szükséges

t

időt.
Bár az integrál kiszámítható,

t

nagyságának megbecsüléséhez elegendő, ha a

\begin{matrix} t \approx \frac{h}{v_{átl}} \end{matrix}

(5)

kifejezést használjuk, ahol

v_{átl}

átlagsebességének a kezdeti

0

és a végső

\begin{matrix} v = \sqrt[]{2 γ M (\frac{1}{R} - \frac{1}{R + h})} = 1, 64 \cdot 10^{- 4} m/s \end{matrix}

számtani közepét vesszük. Így

\begin{matrix} t \approx \frac{2 h}{\sqrt[]{2 M γ (\frac{1}{R} - \frac{1}{R + h})}} = 10, 2 óra \end{matrix}

(7)

adódik. (A pontos érték

\begin{matrix} t = {(2 γ M)}^{- 1 / 2} {{[h R (R + h)]}^{1 / 2} + {(R + h)}^{3 / 2} arc tg \sqrt[]{h / R}} = 10, 7 óra) . \end{matrix}

Ez alatt az idő alatt az űrhajó kereken

6000

km-t tesz meg.
Amikor a "kitett tárgy'' egy űrhajós, aki pisztolyából igen rövid idő alatt

m_{g}

tömegű

v_{g}

sebességű gázt lő ki, tömege

m_{g}

-vel csökken, de

m_{g} v_{g}

nagyságú impulzusra, azaz

\begin{matrix} v = \frac{m_{g} v_{g}}{m - m_{g}} = 0, 5 m/s \end{matrix}

(8)

sebességre tesz szert. Ez a sebesség lényegesen nagyobb, mint az, amelyre a gravitáció gyorsítaná, tehát emellett a

v

mellett a vonzás miatt fellépő sebességnövekedés elhanyagolható. Ezzel a sebességgel a

h = 3 m

utat 6 s alatt teszi meg az űrhajós. Eközben az űrhajó 9,75 km-t tesz meg.

Fehér Péter (Budapest, Kaffka M. Gimn. III. o. t.)

II. megoldás. A kitett test becsapódásának az idejét meghatározhatjuk a Kepler-törvények segítségével is. Képzeljük el, hogy a kitett testet egy igen kicsiny, a két test középpontját összekötő egyenesre

(A B)

merőleges

v_{⊥}

sebességgel indítjuk! Ekkor a pálya egy nagyon elnyújtott ellipszis lesz, amely a

v_{⊥} \to 0

határesetben rázsugorodik az

\bar{A B}

szakaszra (l. az 1. ábrát).

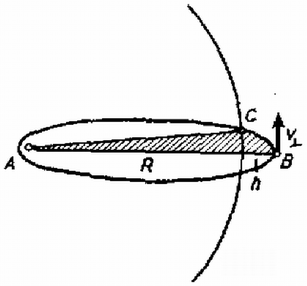1. ábra

Kepler II. törvénye értelmében a

\bar{B C}

szakasz befutásához szükséges idő

(t)

és a teljes keringési idő

(T)

aránya megegyezik a vezérsugár által súrolt felület

(F_{A B C})

és az ellipszis teljes területének

(F_{ell})

arányával:

\begin{matrix} \frac{t}{T} = \frac{F_{A B C}}{F_{ell}} . \end{matrix}

(9)

v_{⊥} \to 0

esetén (9) bal és jobb oldalának határértéke egyenlő. Ebben a határesetben

t

éppen az általunk meghatározni kívánt becsapódási idő,

T

pedig az

R + h

nagytengelyű ellipszisen való keringési idő:

\begin{matrix} T = 2 π \sqrt[]{\frac{{(\frac{R + h}{2})}^{3}}{γ M}} . \end{matrix}

(10)

Kérdés azonban, mi a jobb oldal határértéke

v_{⊥} \to 0

esetén. Ezt a határértéket az ellipszisek következő tulajdonsága alapján kaphatjuk meg: minden

2 a

nagytengelyű ellipszis előállítható úgy, hogy egy

a

sugarú kört az egyik átmérőjére merőlegesen megadott arányban zsugorítunk (2. ábra).

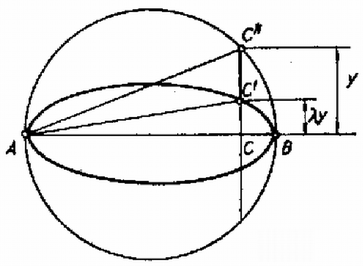2. ábra

Ezen zsugorítás közben (mivel csak egy lineáris méretet változtatunk) a területek ugyanilyen arányban változnak:

\begin{matrix} F_{ell} = λ F_{kör} \end{matrix}

(11)

\begin{matrix} F_{A B C'} = F_{A B C''} . \end{matrix}

(12)

(11) és (12)-ből osztással kapjuk, hogy

\begin{matrix} \frac{F_{A B C'}}{F_{ell}} = \frac{F_{A B C''}}{F_{kör}} \end{matrix}

(13)

λ

-tól függetlenül, tehát a

λ \to 0

esetben is. Így

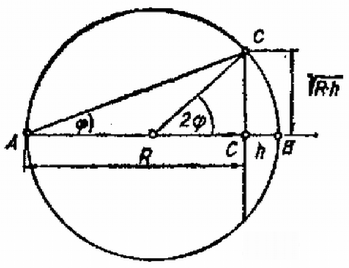\begin{matrix} \frac{t}{T} = \frac{F_{A B C''}}{F_{kör}} \end{matrix}

(14)

3. ábra

(14) jobb oldalát a 3. ábra segítségével könnyen meghatározhatjuk:

\begin{matrix} φ = arc tg \sqrt[]{h / R}, \end{matrix}

(15)

\begin{matrix} F_{A B C''} = \frac{1}{2} \frac{R + h}{2} \sqrt[]{R h} + \frac{2 φ}{2 π} π {(\frac{R + h}{2})}^{2}, \end{matrix}

(16)

\begin{matrix} F_{kör} = π {(\frac{R + h}{2})}^{2}, \end{matrix}

(17)

és így

\begin{matrix} t = \frac{{[h R (R + h)]}^{1 / 2} + {(R + h)}^{3 / 2} arc tg \sqrt[]{h / R}}{{(2 γ M)}^{1 / 2}} \end{matrix}

(18)

Kuna János (Törökszentmiklós, Bercsényi M. Gimn., III. o. t.)
dolgozata alapján

Megjegyzések. 1. Megoldásunk során úgy vettük, hogy az űrhajó a közös súlyponthoz rögzített koordináta-rendszerben áll. Ha figyelembe vesszük, hogy a tömegvonzás őt is gyorsítja, képleteinkben mindenütt

M

helyébe

M + m

kerül.
2. Feladatunk megoldásakor lényegesen kihasználtuk, hogy a tárgyat az űrhajó pályája mentén (elé vagy mögé) rakták ki. Ebben és csakis ebben az esetben fogadható el az a közelítés, hogy az űrhajót és a testet pályán tartó Föld hatását nem vesszük figyelembe. Ennek szemléltetésére vizsgáljuk meg, mi történik, ha a testet pl. az űrhajó és a Föld közé tesszük ki! A feladatban megadott sebesség

r = \frac{γ M_{föld}}{v^{2}} = 1, 57 \cdot 10^{8}

m sugarú körpályának felel meg. Tegyük fel, hogy a tárgyat úgy helyezzük ki az

r - d

(

d = 22

m) sugarú pályára, hogy a sebessége az új pályasugárnak megfelelő

v' ≅ v + {d v}^{3} / (γ M_{föld})

legyen. Ha az űrhajó és a kitelt test nem vonzanák egymást, a két test koncentrikus pályán haladna, de a kitett test a saját pályáján

{d v}^{3} / (γ M_{föld}) ≅ 2, 4 \cdot 10^{- 4}

m/s sebességgel gyorsabban futna. Erre a mozgásra szuperponálódik a kölcsönös vonzás hatása. Mivel az ebből eredő sebesség azonos nagyságrendű a két test sebességkülönbségével, azt látjuk, hogy a test ‐ miközben közeledik az űrhajóhoz ‐ egy kicsit (nem elhanyagolható mértékben!) előre is szalad, és az űrhajó felületét nem három méter befutása után éri el.
Más típusú probléma merül fel, ha azt feltételezzük, hogy a kitett test és az űrhajó sebessége az indításkor teljesen azonos. A kisebb sugáron a körpályán maradáshoz szükséges sebesség nagyobb

(v' > v)

, mint amivel a test rendelkezik, így az űrhajó vonzása nélkül a kitett test közeledne a Földhöz, azaz távolodna az űrhajótól. Megvizsgálva a fellépő gyorsulások nagyságrendjét

[

az űrhajó Föld felé mutató (centripetális) gyorsulásánál a kis test gyorsulása

\frac{2 γ M d}{r^{3}} = 4 \cdot 6 \cdot 10^{- 9} {m/s}^{2}

értékkel nagyobb

]

, azt találjuk, hogy még az űrhajó vonzása sem elegendő ahhoz, hogy az űrhajó és a kitett test távolodását megakadályozza.
A 2. megjegyzés jól mutatja, hogy milyen gondosan kell eljárnunk, amikor több test egymás gravitációs terében való mozgását vizsgáljuk. Ezért találtuk érdemesnek a probléma részletes tárgyalását közölni, ezt egy külön cikkben találja meg az érdeklődő olvasó (l. a 225. oldalt).