Feladat:	1665. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Halász Péter
Füzet:	1981/március, 135 - 136. oldal		PDF  |  MathML
Témakör(ök):	Rugalmatlan ütközések, Nagy kitérítés, Hő, Feladat
Hivatkozás(ok):	Feladatok: 1980/október: 1665. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.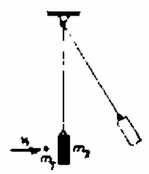 a) A mennyezetről lelógó test impulzusa kezdetben nulla, és egy golyó belövése $m_1{v}_1$-gyel növeli a rendszer impulzusát. Így $n$ golyócska belelövése után az impulzus $n\left(m_1{v}_1\right)$ lesz. A test sebességét jelöljük ekkor $u_n$,-nel. Felírhatjuk az impulzusmegmaradást: $\begin{array}{c}{\displaystyle u_n=\frac{n\left(m_1{v}_1\right)}{m_2+n{m}_1}=\frac{m_1{v}_1}{\left(m_2/n\right)+m_1}}\end{array}$ Láthatjuk, hogy ez a függvény szigorúan monoton növekedő, így a maximális sebességet $n\to \infty$ esetben kapjuk meg: $\underset{n\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}{u}_n=v_1=15\text{ m/s}$. Az inga lengésére írjuk fel a mechanikai energia megmaradását (az $n$-edik golyócska belövése után) $\begin{array}{c}{\displaystyle \left(1/2\right)\left(m_2+n{m}_1\right)u_n^2=\left(m_2+n{m}_1\right)gh\mathrm{,}}\end{array}$ ahol $h$ az inga legnagyobb magassága; $\begin{array}{c}{\displaystyle h=u_n^2/2g\mathrm{,}\text{tehát}{h}_{max}=v_1^2/2g=11\mathrm{,}25\text{ m}\mathrm{.}}\end{array}$ Tebát az inga legfeljebb $11\mathrm{,}25$ m magasra emelkedhet.   b) Az $n$-edik golyó belövése után a rendszerrel összesen $E_1=n{m}_1{v}_1^2/2$ energiát közöltünk. Az ütközés utáni pillanatban helyzeti energiája még nincs, így összes mechanikai energiája a mozgási energia: $\begin{array}{c}{\displaystyle E_2=\frac{\left(m_2+n{m}_1\right)u_n^2}{2}\mathrm{.}}\end{array}$ A két energia különbsége fordítódott arra, hogy a rendszer hőmérsékletét emelje. Az ismert összefüggés alapján a hőmérsékletemelkedés: $\begin{array}{c}{\displaystyle \Delta T_n=\frac{Q}{c\left(m_2+n{m}_1\right)}=\frac{E_1-E_2}{c\left(m_2+n{m}_1\right)}\mathrm{.}}\end{array}$ Egyszerűsítések után: $\begin{array}{c}{\displaystyle \Delta T_n=\frac{n{m}_1{m}_2{v}_1^2}{2c{\left(m_2+n{m}_1\right)}^2}=\frac{m_1{m}_2{v}_1^2}{2c}\cdot \frac{1}{\frac{{\left(m_2+n{m}_1\right)}^2}{n}}\mathrm{.}}\end{array}$ A $\Delta T$ ott maximális, ahol a $\begin{array}{c}{\displaystyle \frac{{\left(m_2+n{m}_1\right)}^2}{n}=\frac{m_2^2}{n}+2m_1{m}_2+n{m}_1^2}\end{array}$ kifejezésnek minimuma van. A számtani és mértani középre vonatkozó összefüggést felhasználva írhatjuk, hogy $\begin{array}{c}{\displaystyle \frac{m_2^2}{n}+n{m}_1^2\ge 2m_1{m}_2\mathrm{.}}\end{array}$ A bal oldatnak tehát $n$ függvényében minimuma akkor van, ha az egyenlőség teljesül, azaz $\begin{array}{c}{\displaystyle \frac{m_2^2}{n}=n{m}_1^2\mathrm{.}}\end{array}$ amiből $\begin{array}{c}{\displaystyle n=\frac{m_2}{m_1}=24.}\end{array}$ Ezt felhasználva kapjuk, hogy $\begin{array}{c}{\displaystyle \Delta T_{max}=\Delta T_{24}=0\mathrm{,}035\text{ K}\mathrm{.}}\end{array}$    Halász Péter (Miskolc, Földes F. Gimn., IV. o. t.)