Kezdőlap


Feladat:	1660. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bene László , Horváth Gábor , Kaptás Dénes , Krähling János , Mocsáry Géza , Tarcsay Miklós , Várhelyi Tamás
Füzet:	1981/február, 92 - 94. oldal		PDF \| MathML
Témakör(ök):	Coulomb-törvény, Tömegpont egyensúlya, Egyéb kényszermozgás, Feladat
Hivatkozás(ok):	Feladatok: 1980/szeptember: 1660. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Helyezzük a parabolát egy koordináta‐rendszerbe úgy, hogy az $y$ tengely legyen a parabola tengelye és az $x$ tengely érintse. Ekkor a parabola egyenlete: 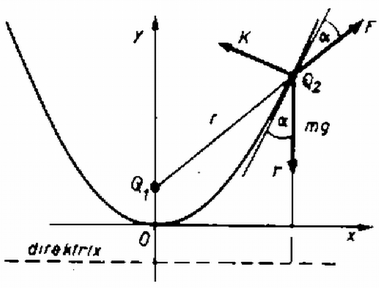$y = (1 / 4 cm) \cdot x^{2}$ .
A golyócskára három erő hat: a nehézségi erő, a Coulomb‐erő és a parabola érintőjére merőleges kényszererő.
Geometriából ismeretes, hogy a parabola egy pontjába húzott vezérsugár és ugyanezen ponton átmenő, a tengellyel párhuzamos egyenes azonos szöget zár be a görbe érintőjével, tehát az ábrán $α$ -val jelölt szögek azonosak.

Az egyensúly feltétele, hogy a nehézségi erő és a Coulomb‐erő eredője merőleges legyen a parabola érintőjére, tehát

\begin{matrix} m g cos α = F cos α \end{matrix}

legyen. Ez az egyenlőség akkor áll fenn, ha

m g = F

, vagy ha

α = 90^{\circ}

. Az utóbbi eset akkor lehetséges, ha a golyó a (0; 0) koordinátájú pontban van. Most foglalkozzunk az előbbi esettel. A Coulomb törvény segítségével

r

kiszámítható:

\begin{matrix} m g = \frac{k Q_{1} Q_{2}}{r^{2}}, \end{matrix}

azaz

\begin{matrix} r = \sqrt[]{\frac{k Q_{1} Q_{2}}{m g}} . \end{matrix}

Felhasználva, hogy

y + 1 cm = r

és hogy

y = (1 / 4 cm) \cdot x^{2}

, a golyó koordinátáit is megkapjuk:

\begin{matrix} y = \sqrt[]{\frac{k Q_{1} Q_{2}}{m g}} - 1 cm; x = \pm \sqrt[]{4 cm \sqrt[]{\frac{k Q_{1} Q_{2}}{m g}} - 4 {cm}^{2}} . \end{matrix}

Számadatainkkal:

r = 5 cm

x = \pm 4 cm

y \pm 4 cm

.
A (4; 4) és a (

- 4

; 4) pontokban a golyó stabil egyensúlyi helyzetben van, hiszen ha feljebb, ill. lejjebb csúszik, akkor az

F

erő csökken, ill. nő, míg a nehézségi erő állandó marad, így az eredő erő lefelé, ill. felfelé fogja mozgatni.
A golyó a (0; 0) pontban labilis egyensúlyi állapotban van, hiszen itt

F > m g

, ezért innen kimozdítva az eredő erő a parabola szárain felfelé fogja mozgatni.
Vizsgáljuk meg, mi a helyzet tetszőleges töltések esetén. Ha ezek azonos előjelűek, akkor ugyanaz a helyzet, mint
eddig, de most

r < 1 cm

nem lehetséges, ezért a két oldalsó egyensúlyi állapot csak

\begin{matrix} \frac{k Q_{1} Q_{2}}{m g} > 1 cm \end{matrix}

esetén valósul meg, és ha

\frac{k Q_{1} Q_{2}}{m g} \leq 1

cm, akkor a (0; 0) pontban lesz csak egyensúlyi helyzet, viszont ez stabilis.
Ha különböző előjelűek a töltések, akkor nyilván csak a (0; 0) pontban van egyensúlyban a golyó, hiszen akkor van legmélyebben és a

Q_{1}

töltéshez legközelebb.
Mivel a feladat szövegéből nem derül ki, hogy a parabola szárai felfelé vagy lefelé állnak, vizsgáljuk meg, mi a helyzet az utóbbi esetben. Ha a töltések azonos előjelűek, akkor ugyanaz a helyzet, mint korábban a különböző előjelű töltések esetén, de a (0; 0) hely labilis egyensúlyi állapot. Ha pedig a töltések különböző előjelűek, akkor hasonló lesz a helyzet, mint a megoldás első részében, azzal a különbséggel, hogy

- \frac{k Q_{1} Q_{2}}{m g} > 1

esetén valósul meg a két oldalsó egyensúlyi állapot, amely most labilis lesz, és az origóban lesz a golyó stabil egyensúlyban, valamint

- \frac{k Q_{1} Q_{2}}{m g} \leq 1

esetén csak az origóban lesz egyensúlyban, és ez az állapot labilis lesz.

Horváth Gábor (Kiskunhalas, Szilády Á. Gimn., IV. o. t.)

II. megoldás. Vizsgáljuk meg a rendszer energiaviszonyait! A helyzeti energia 0-szintjét a direktrixhez rögzítsük. Ekkor az elektromosan töltött golyócska helyzeti energiája csak

r

-től függ, és két részből tevődik össze:

\begin{matrix} E (r) = m g r + \frac{k Q_{1} Q_{2}}{r}, ahol r \geq 1 cm . \end{matrix}

A golyócska ott lesz egyensúlyban, ahol helyzeti energiájának (legalább lokális) szélsőértéke van.

r

szerint deriválva kapjuk:

\begin{matrix} E' (r) = m g - \frac{k Q_{1} Q_{2}}{r^{2}} . \end{matrix}

E (r)

-nek ott lehet szélsőértéke, ahol

E' (r) = 0

vagy az értelmezési tartomány végpontjában lehet szélsőérték. Az előbbi feltétel így írható:

\begin{matrix} 0 = m g - \frac{k Q_{1} Q_{2}}{r^{2}}, \end{matrix}

innen

r

-et kifejezve

\begin{matrix} r = \sqrt[]{\frac{k Q_{1} Q_{2}}{m g}} . \end{matrix}

Erről könnyen meg lehet mutatni, hogy az adott számadatok esetén minimumhely. Az értelmezési tartomány végpontjában,

r = 1 cm

-nél pedig lokális maximum van.

Tehát

r = 1

cm vagy

r = \sqrt[]{\frac{k Q_{1} Q_{2}}{m g}}

esetén lesz a golyó egyensúlyban. A megoldás innen ugyanúgy folytatható, mint az I. megoldás esetében.

Mocsáry Géza (Pannonhalma, Bencés Gimn., IV. o. t.)
dolgozata alapján