| Feladat: | 1657. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Jeney Tamás , Károlyi Gyula , Lóczy Géza , Oszlányi Gábor | ||
| Füzet: | 1981/február, 89 - 90. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Egyéb merev test síkmozgások, Csúszó súrlódás, Súrlódási határszög, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1980/szeptember: 1657. fizika feladat | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.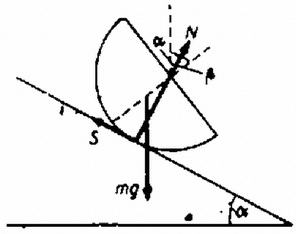 A félgömb nem csúszik meg a lejtőn, ha a rá ható erők eredője nulla. A lejtő nyomóereje (N) és a súrlódási erő (S) az ábra alapján: A tapadás feltételébe beírva a szokásos
Vizsgáljuk meg most azt az esetet, amikor és a félgömb tisztán csúszik! Ekkora félgömb a lejtővel párhuzamos gyorsulással mozog, szimmetriatengelyének a lejtőre bocsátott merőlegessel bezárt szöge állandó. Írjuk fel Newton II. törvényét a lejtővel párhuzamos és az arra merőleges összetevőkre: ahol a csúszás miatt
Ha a félgömböt egy súlytalan másik félgömbbel teljes gömbbé egészíthetjük ki, amelynek súlypontja középpontjától távolságra van, mindkét értékének fizikai értelem tulajdonítható: a pozitív előjelhez tartozó megoldás stabil, a negatív instabil helyzetnek felel meg. Félgömb esetében , különben a félgömb sík lapjára billen. akkor lesz a negatív előjelet véve is pozitív, ha , ahonnan . Összefoglalva, ha és így a félgömb csúszik, szimmetriatengelyének a függőlegessel bezárt szöge
Jeney Tamás (Miskolc, Földes F. Gimn., III. o. t.) dolgozata alapján |