Feladat: 1643. fizika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Horváth Gábor 
Füzet: 1981/január, 37 - 38. oldal  PDF  |  MathML 
Témakör(ök): Egyéb párhuzamos erők eredője, Rugalmas erő, Arkhimédész törvénye, Feladat
Hivatkozás(ok):Feladatok: 1980/április: 1643. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.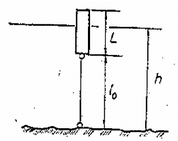

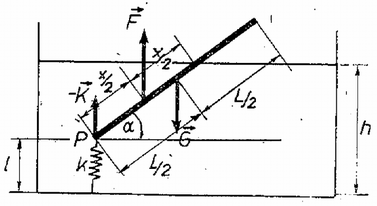Jellemezzük a rúd helyzetét a vízszintessel bezárt α szöggel és azon végpontjának az edény aljából való távolságával (l), amihez a rugót erősítettük.
a)h≤l0=30cm esetén a rugalmast szál laza, a rúd úszik a felszínen, tehát α=0 és l=h.
b)h>l0 a rugó már feszes, és a rúd x hosszúságú darabja a víz alatt van. A rúdra ható G=ALϱg nagyságú súlyerőt, az F=Axϱvg nagyságú felhajtóerőt, valamint a K=k(l-l0) nagyságú rugóerőt és ezek támadáspontját az 1. ábra szemlélteti.
 

1. ábra
 

Mivel G és F hatásvonala függőleges, az egyensúly szükséges feltétele hogy K hatásvonala is ilyen irányú legyen.
A ΣF=0 és a ΣM=0 egyensúlyi feltételek (az utóbbi a P pontra) felírva:
G+K-F=ALϱg+k(l-l0)-Axϱvg=0,(1)F(x/2)cosα-G(L/2)cosα=(x2/2)Aϱvgcosα-(L2/2)Aϱgcosα=0.(2)


Ezenkívül az ábráról leolvasható, hogy
l+xsinα=h.(3)

Tegyük fel egyelőre, hogy cosα≠0, ekkor a fenti egyenletrendszer megoldása:
x=Lϱ/ϱv=77,5cm,(4a)l=l0+ALϱgk(ϱvϱ-1)=31,8cm(4b)sinα=h-[l0+ALϱgk(ϱvϱ-1)]Lϱϱv=1,3⋅10-2cm-1⋅h-0,41.(4c)


Mivel 0≤sinα≤1, a fenti megoldás csak a 31,8cm≤h≤109,3cm szintmagasságokra érvényes.
Érdekes ezt összevetni az a) esettel, ahol 0≤h≤30cm. Úgy tűnik, hogy 30cm<h<31,8cm esetén a rúd helyzetéről semmit sem tudunk mondani. Ennek oka az, hogy nagyon kis α szögek esetén a (2) egyenlet felírásánál használt vékony rúd közelítés nem igaz (l. 2. ábrát).
 

2. ábra
 

c)h>109,3cm esetén a rúd már függőleges,
teljes elmerüléséig az egyensúly feltétele az (1)‐(3) egyenlet (most sinα=1), amelynek megoldása
l=Aϱvg⋅(h-Lϱϱv)+kl0k+Aϱvg=9⋅10-2h+21,8  cm  (5)α=90∘.


A rúd akkor merül el, ha h-l=L, vagyis (5) alapján h=133,8cm-es vízmagasságnál.
d)h>133,8cm esetén a felhajtóerő állandó, ezért a rugóerő sem nő tovább. Ekkor (5)-ből
l=33,8cm,α=90∘.
Az l(h),α(h) függvények menetét a)‐c) pontok alapján a 3. ábra tünteti fel.
 

3. ábra
 
Térjünk vissza ezek után a (2) egyenlethez. Látjuk, hogy ez akkor is teljesül, ha cosα=0, vagyis α=90∘. Ez azt jelenti, hogy létezik az eddigiektől különböző megoldása az (1) ‐(3) egyenletrendszernek, amikor is a rúd végig függőleges helyzetű.
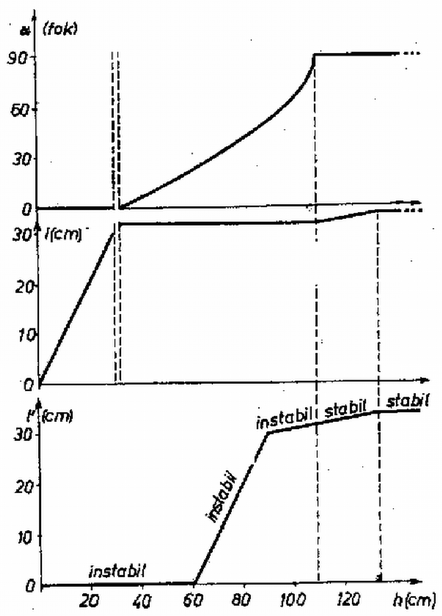Ezt a helyzetet (elvileg) úgy valósíthatjuk meg, hogy a rudat az edény aljára állítjuk, majd megkezdjük a víz betöltését. A továbbiakban röviden vizsgáljuk meg ezt az esetet is !
A)A rúd akkor kezd el úszni, amikor F=G, vagyis (ϱ/ϱv=0,6 miatt) amikor 0,6 része már víz alatt van. Ezért 0≤h<h0=60cm esetén l'=0.
B)h0<h≤h0+l0=90cm vízmagasság mellett a rugó még laza, ekkor
l'=h+h0.
C)h>h0+l0 esetén egészen a teljes elmerülésig a rúd helyzetét a (5) függvény írja le.
D)Megegyezik a d) pontban leírtakkal.
 

Az l'(h) függvényt szintén a 3. ábrán szemléltettük.
 

 Horváth Gábor (Kiskunhalas, Szilády Á. Gimn., III. o. t.)
 

Megjegyzés. A rúd függőleges helyzete nem minden esetben stabilis. Az 1. ábra alapján beláthatjuk, hogy ehhez az szükséges, hogy F(x/2)>G(l/2) legyen. A (4a) képlet szerint ez akkor következik be, ha x>Lϱ/ϱv=77,5cm, vagyis ‐ (5) alapján ‐ ha h>109,3cm.