Kezdőlap


Feladat:	1624. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bedey György , Benedek Tibor , Guba Kornél , Ivánfi Ádám , Jeney Tamás , Kuna János , Miletics Edit , Oszlányi Gábor , Sándor Ferenc
Füzet:	1980/november, 175 - 177. oldal		PDF \| MathML
Témakör(ök):	Hajítások, Tökéletesen rugalmatlan ütközések, Feladat
Hivatkozás(ok):	Feladatok: 1980/február: 1624. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vegyünk fel a függőleges síkban egy derékszögű koordináta-rendszert és indítsuk az $M$ tömegű testet ennek origójából. Az origótól $d$ távolságban az $M$ tömegű test $h$ magasságot ér el.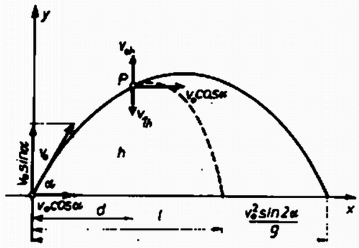

A ferde hajítás pályaegyenletéből

\begin{matrix} h = d \cdot tg α - \frac{g d^{2}}{2 v_{0}^{2} cos^{2} α} . \end{matrix}

(1)

Ütközés előtt a

P

pontban az

M

tömegű test sebességének vízszintes és függőleges komponense

\begin{matrix} v_{0 x} = v_{0} cos α; v_{0 h} = \pm \sqrt[]{v_{0}^{2} sin^{2} α - 2 g h}; & (2) \end{matrix}

a függőlegesen feldobott

m

tömegű test sebességkomponensei:

\begin{matrix} v_{1 x} = 0; v_{1 h} = \pm \sqrt[]{v_{1}^{2} - 2 g h} \end{matrix}

(3)

A két test rugalmatlan ütközés után közös sebességgel folytatja útját, amelynek komponenseit jelölje

u_{x}

, ill.

u_{y}

Az impulzusmegmaradás törvényéből:

\begin{matrix} M v_{0 x} = (M + m) u_{x}; M v_{0 h} + m v_{1 h} = (M + m) u_{y} . \end{matrix}

(4)

(4)-ből (2) és (3) felhasználásával kapjuk:

\begin{matrix} u_{x} = \frac{M v_{0} cos α}{M + m}; & (5) \\ u_{y} = \frac{\pm M \sqrt[]{v_{0}^{2} sin^{2} α \pm 2 g h} \pm m \sqrt[]{v_{1}^{2} - 2 g h}}{M + m} . & (6) \end{matrix}

Vizsgáljuk meg a kapott (6) kifejezést! A számlálóban mindkét tag előtt bármelyik előjel állhat, így

u_{y}

-ra négy különböző érték adódik. Vegyük sorra ezek fizikai jelentését!

0 < d < \frac{v_{0}^{2} sin 2 α}{2 g}

esetén (a két test az

M

tömegű test pályájának felszálló ágában találkozik) az előjelek (

+

+

), ill. (

+

-

) aszerint, hogy az

m

tömegű test "alulról'' vagy " felülről'' ütközik az

M

tömegű testbe. Az ábrán az utóbbit rajzoltuk fel.

\frac{v_{0}^{2} sin 2 α}{2 g} < d < \frac{v_{0}^{2} sin 2 α}{g}

esetén (a két test a

M

tömegű test pályájának leszálló ágában ütközik), az előjelek a fentieknek megfelelően (

-

+

), ill. (

-

-

).
A két test találkozásának szükséges feltétele:

\begin{matrix} 0 \leq d \leq \frac{v_{0}^{2} sin 2 α}{g} . \end{matrix}

Megjegyezzük, hogy lehetséges

d = 0

d = \frac{v_{0}^{2} sin 2 α}{g}

és

d = \frac{v_{0}^{2} sin 2 α}{2 g}

megválasztása is a feladat paramétereinek. Ezek azt jelentik, hogy a két test rendre az

M

tömegű test pályájának kezdő-, vég-, ill. tetőpontjában ütközik. Ezek a lehetőségek azonban nyilván bennfoglaltatnak az (5) képletben, ui. akkor rendre

h = 0

h = v_{0}^{2} sin^{2} α / 2 g

h = 0

.
Nézzük meg ezek után, hogy az origótól milyen

l

távolságban ér földet a két test! Ütközés után a vízszintes és függőleges elmozdulás:

\begin{matrix} x = d + u_{x} \cdot t, & (7) \\ y = h + u_{y} \cdot t - (g / 2) t^{2} . & (8) \end{matrix}

(7)-ből és (8)-ból

t

kiküszöbölésével kapjuk a következő pályaegyenletet:

\begin{matrix} y - h = \frac{u_{y}}{u_{x}} (x - d) - \frac{g}{2 u_{x}^{2}} {(x - d)}^{2} . \end{matrix}

(9)

Földetéréskor

x = l

y = 0

, amit (9)-be helyettesítve kapjuk, hogy

\begin{matrix} l = d + \frac{u_{x}}{g} (u_{y} + \sqrt[]{u_{y}^{2} + 2 g h}), \end{matrix}

ahol

h

u_{x}

u_{y}

rendre az (1), (5) és (6) kifejezések által adott. Mivel mindig

l > d

, ezért (9) másik megoldásának nincs fizikai értelme.

Jeney Tamás (Miskolc, Földes F. Gimn., II. o. t.)

Megjegyzés. A függőleges impulzus-komponensekre a (4) megmaradási törvény csak akkor igaz (ütközéskor a belső erőkön kívül hat a nehézségi erő is), ha az ütközést pillanatszerűnek tételezzük fel.
Ha ui. az ütközéskor működő belső erők abszolút értékét

F

-fel jelöljük, akkor ütközéskor a mozgásegyenletek

\begin{matrix} \frac{Δ (M v_{0 h})}{Δ t} & = - M g + F, \\ \frac{Δ m (v_{1 h})}{Δ t} & = - m g - F . \end{matrix}

A két egyenletet összeadva kapjuk, hogy

\begin{matrix} Δ (M v_{0 h} + m v_{1 h}) = - (M + m) g Δ t . \end{matrix}

Látható, hogy

Δ t \to 0

esetén valóban

Δ (M v_{0 h} + m v_{1 h}) = 0

Oszlányi Gábor (Miskolc, Földes F. Gimn., II. o. t.)