Kezdőlap


Feladat:	1612. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Glück Ferenc , Golovics István , Horváth Gábor , Horváth Viktor , Hudi István , Jilling Ferenc , Krähling János , Pöltl János Tamás , Sárközi Imre , Várhelyi Tamás
Füzet:	1980/szeptember, 41 - 43. oldal		PDF \| MathML
Témakör(ök):	Egyenesvonalú mozgás lejtőn, Csúszó súrlódás, Gördülés lejtőn, Nyomóerő, kötélerő, Tapadó súrlódás, Munkatétel, Feladat
Hivatkozás(ok):	Feladatok: 1979/december: 1612. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először határozzuk meg a golyó gyorsulását! A golyóra súlyereje, a lejtő nyomóereje és a súrlódási erő hat (1. az ábrát). A golyó tömegközéppontja a lejtőre merőlegesen nem gyorsul, lejtő irányú gyorsulása 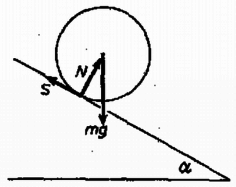$a$ .

Newton II. törvényéből

\begin{matrix} m g cos α - N = 0, & (1) \\ m g sin α - S = m a . & (2) \end{matrix}

A forgómozgás alapegyenlete:

\begin{matrix} S r = θ β = (2 / 5) m r^{2} β . \end{matrix}

(3)

1. Ha a gömb csúszás nélkül gördül, akkor

\begin{matrix} a_{1} = β_{1} r . \end{matrix}

(4)

A (2)-(4) egyenletekből a gyorsulás:

\begin{matrix} a_{1} = β_{1} r = (5 / 7) g sin α \approx 3,57 {m/s}^{2} . \end{matrix}

(5)

A tapadás feltétele (1), (3) és (4) alapján

\begin{matrix} S = (2 / 5) m a_{1} ≦ μ N = μ m g cos α, \end{matrix}

ahonnan (5) folytán

\begin{matrix} μ ≧ μ_{0} = (2 / 7) tg α = 0,165. \end{matrix}

(6)

2. Ha ez a feltétel nem áll fenn, a gömb csúszva gördül. Ekkor csúszó súrlódás lép fel, tehát

\begin{matrix} S = μ N = μ m g cos α, & (7) \\ a_{2} = g sin α - μ g cos α, & (8) \\ β_{2} = \frac{5 μ g cos α}{2 r} & (9) \end{matrix}

Vizsgáljuk most meg, hogyan mozog a golyó a feladatban adott lejtőn!
Két eset lehetséges:
a) Ha mindkét tapadási súrlódási együttható nagyobb vagy egyenlő

μ_{0}

-lal, akkor a golyó az egész lejtőn tisztán gördül. Ez elképzelhető, mivel a tapadó súrlódási együttható nagyobb a csúszónál, így lehetséges, hogy bár

μ_{2} = 0,1

, a tapadó súrlódásra

μ_{2 t} ≧ 0,165

.
Dinamikai számolás helyett alkalmazzuk most az energiamegmaradás törvényét! Súrlódási veszteség ekkor nincs, hiszen a golyó lejtővel érintkező pontjánál a golyó és a lejtő között nincs elmozdulás:

\begin{matrix} m g (2 s) sin α = (1 / 2) m v^{2} + (1 / 2) θ ω^{2} = \\ = (1 / 2) m v^{2} + (1 / 2) \cdot (2 / 5) m r^{2} v^{2} / r^{2} . \end{matrix}

(10)

Innen a lejtő alján a golyó sebessége:

\begin{matrix} v = \sqrt[]{(20 / 7) s g sin α} \approx 3,78 m/s . \end{matrix}

(11)

Mivel a golyó sehol nem csúszik meg, eredményünk független a súrlódási együtthatóktól, így azok felcserélésétől is.
b) Ha azon a szakaszon, ahol

μ_{2} = 0,1

, a tapadó súrlódási együttható is kisebb

μ_{0}

-nál, akkor ezen a szakaszon a golyó megcsúszik. A felső

s

hosszúságú szakaszon csúszásmentes gördülés történik

a_{1}

gyorsulással. A lejtő közepén a golyó sebessége és szögsebessége:

\begin{matrix} v_{1} & = \sqrt[]{2 a_{1} s} \approx 2,67 m/s, \\ ω_{1} & = v_{1} / r \approx 26,71 1/s . \end{matrix}

A lejtő második felén a golyó megcsúszik, gyorsulása (8)-ból

a_{2} \approx 4,13 {m/s}^{2}

, szöggyorsulása (9)-ből

β_{2} \approx 21,7 {1/s}^{2}

. Legyen

t_{2}

a lejtő közepétől a leérésig eltelt idő. Ekkor a haladó mozgásra

\begin{matrix} s & = v_{1} t_{2} + (a_{2} / 2) t_{2}^{2}, \\ v_{2} & = v_{1} + a_{2} t_{2} . \end{matrix}

Ezekből az egyenletekből a leérésig elért sebesség:

\begin{matrix} v_{2} = \sqrt[]{v_{1}^{2} + 2 a_{2} s} \approx 3,93 m/s . \end{matrix}

A második szakasz megtételéhez szükséges idő

\begin{matrix} t_{2} \approx 0,303 s, \end{matrix}

a végső szögsebesség

\begin{matrix} ω_{2} = β_{2} t_{2} + ω_{1} \approx 33,3 1/s . \end{matrix}

A súrlódási munkából származó energiaveszteség a golyó lejtővel érintkező pontjának a lejtőhöz viszonyított elmozdulásával arányos. Ez az elmozdulás a lejtő második szakaszának hossza és az elfordulásból származó kerületi elmozdulás különbsége. A súrlódási munka tehát

\begin{matrix} W = μ_{2} m q cos α [s - (β_{2} / 2) t_{2}^{2} r - ω_{1} t_{2} r] \approx 0,078 J . \end{matrix}

Eredményünk ellenőrizhető a munkatétel alapján:

\begin{matrix} m g (2 s) sin α = (1 / 2) m v_{2}^{2} + (1 / 2) θ ω_{2} + W . \end{matrix}

Cseréljük fel a súrlódási együtthatókat! Ekkor az első szakaszon lesz csúszva gördülés

a_{2}

gyorsulással és

β_{2}

szöggyorsulással. A lejtő közepén a sebesség

\begin{matrix} v_{3} = \sqrt[]{2 s a_{2}} \approx 2,88 m/s, \end{matrix}

az indulástól eltelt idő

\begin{matrix} t_{3} = \sqrt[]{2 s / a_{2}} \approx 0,696 s, \end{matrix}

az elért szögsebesség

\begin{matrix} ω_{3} \approx β_{2} t_{2} \approx 15,1 1/s . \end{matrix}

Az alsó szakaszon ugyan teljesül

μ_{1} > μ_{0}

összefüggés, azonban

v_{3} > ω_{3} r

, így a golyó egy

s_{4}

hosszúságú szakaszon köszörülni fog. A gyorsulás és a szöggyorsulás ekkor (8)-ból és (9)-ből

\begin{matrix} a_{4} \approx 1,54 {m/s}^{2}, β_{4} \approx 86,6 {1/s}^{2} . \end{matrix}

A köszörülés megszűnéséig

t_{4}

idő telik el, ezalatt a golyó sebessége és a kerületi sebesség egyenlővé válik:

\begin{matrix} v_{4} = a_{4} t_{4} + v_{3} = r (β_{4} t_{4} + ω_{3}) . \end{matrix}

Innen

\begin{matrix} t_{4} \approx 0,192 s, v_{4} \approx 3,17 m/s, s_{4} = \frac{v_{3} + v_{4}}{2} t_{4} \approx 0,581 m (< s) . \end{matrix}

A hátralevő

s - s_{4}

hosszúságú szakaszon

a_{1}

gyorsulással gördül a golyó, a végsebesség

\begin{matrix} v_{5} = \sqrt[]{v_{4}^{2} + 2 a_{1} (s - s_{4})} \approx 36,1 m/s, \end{matrix}

kisebb, mint az előző esetben. A különbségért az

s_{4}

szakaszon történő köszörülés a felelős. Súrlódási veszteség most az első és a második szakaszon adódik:

\begin{matrix} W = μ_{2} m g cos α [s - (1 / 2) β_{2} t_{3}^{2}] + μ_{1} m g cos α (s_{4} - r \frac{ω_{3} + ω_{4}}{2} t_{4}) \approx 0,869 J, \end{matrix}

ami a hosszabb köszörülés miatt lényegesen több, mint az előző esetben.

Horváth Gábor (Kiskunhalas, Szilády Á. Gimn., III. o. t.)