Kezdőlap


Feladat:	1605. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Czuczor Judit , Krähling János
Füzet:	1980/április, 188 - 189. oldal		PDF \| MathML
Témakör(ök):	Tehetetlenségi nyomaték, Gördülés lejtőn, Pontrendszerek mozgásegyenletei, Forgási energia, Feladat
Hivatkozás(ok):	Feladatok: 1979/november: 1605. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Határozzuk meg először a gömbhéjnak a középpontjára vonatkozó tehetetlenségi nyomatékát! Legyen a gömbhéj külső sugara $R$ , belső sugara $r$ , anyagának sűrűsége $ϱ$ .

\begin{matrix} Θ_{0} = \frac{2}{5} \cdot \frac{4 π}{3} R^{3} ϱ \cdot R^{2} - \frac{2}{5} \cdot \frac{4 π}{3} r^{3} ϱ \cdot r^{2} = \frac{2}{5} M \cdot \frac{R^{5} - r^{5}}{R^{3} - r^{3}} . \end{matrix}

ahol

M = (4 π / 3)

(R^{3} - r^{3}) ϱ

a gömbhéj tömege. Nagyon vékony gömbhéj esetén

\begin{matrix} Θ = {lim}_{r \to R}^{} Θ_{0} = {lim}_{r \to R}^{} \frac{2}{5} M \frac{(R - r) (R^{4} + R^{3} r + R^{2} r^{2} + R r^{3} + r^{4})}{(R - r) (R^{2} + R r + r^{2})} = \frac{2}{3} M R^{2} . \end{matrix}

(1)

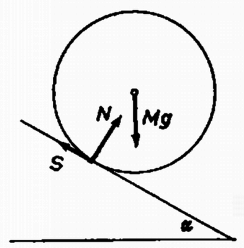1. ábra

Számítsuk ki az üres gömb

a_{0}

gyorsulását! A gömb középpontjának lejtő irányú mozgására és a tömegközéppont körüli forgásra vonatkozó egyenlet, valamint a csúszásmentes gördülést figyelembe vevő kényszerfeltétel (1. ábra):

\begin{matrix} M g sin α - S = M a_{0}, & (2) \\ S R = Θ β, & (3) \\ a_{0} = β R, & (4) \end{matrix}

ahol

β

a szöggyorsulás.
Az (1)‐(4) egyenletekből a gömb gyorsulása

\begin{matrix} a_{0} = (3 / 5) g sin α . \end{matrix}

(5)

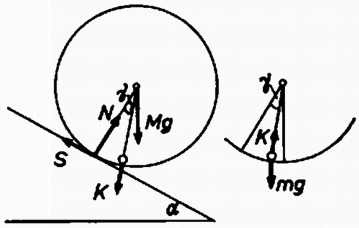2. ábra

Helyezzük az

m

tömegpontot a gömbhéj belsejébe! Ha a gömbhéj egyenletesen, lengések nélkül gyorsul, a tömegpont helyét jellemző

γ

szög a mozgás során nem változik (2. ábra). A tömegpont és a gömbhéj között sugár irányú

K

nagyságú erő hat. A tömegpont ill. a gömbhéj mozgását leíró egyenletek:

\begin{matrix} m g sin α - K sin γ = m a, & (6) \\ M g sin α + K sin γ - S = M a, & (7) \\ S R = Θ β, & (8) \\ α = β R, & (9) \end{matrix}

ahonnan

\begin{matrix} a = \frac{M + m}{(5 / 3) M + m} g sin α . \end{matrix}

(10)

A feladat feltétele szerint

a = 1, 2 a_{0}

, azaz

\begin{matrix} 1, 2 \cdot \frac{3}{5} = \frac{M + m}{(5 / 3) M + m} . \end{matrix}

(11)

Az egyenletet megoldva a tömegpont és a gömb tömegének aránya

\begin{matrix} M / m = 7 / 5. \end{matrix}

Krähling János (Bonyhád, Petőfi S. Gimn., III. o. t.)

II. megoldás. Tegyük fel, hogy a gömbhéj

h

magasságból gördül le a lejtőn. A kezdeti helyzeti energia a gömb mozgási és forgási energiájává ill. a tömegpont mozgási energiájává alakul. Üres gömbre ill., ha a tömegpont a gömb belsejében van:

\begin{matrix} M g h = (1 / 2) M v_{0}^{2} + (1 / 2) Θ ω_{0}^{2}, & (12) \\ (M + m) g h = (1 / 2) M v^{2} + (1 / 2) Θ ω^{2} + (1 / 2) m v^{2}, & (13) \end{matrix}

ahol a tökéletes gördülés miatt

v_{0} = ω_{0} R

és

v = ω R

. Egy

l

úton a gyorsulással mozgó test végsebességére a

v^{2} = 2 a l

összefüggés érvényes, tehát a gyorsulás arányos a sebesség négyzetével. Így a gyorsulás

20 %

-os növekedésére vonatkozó feltétel ekvivalens az

\begin{matrix} 1, 2 \cdot v_{0}^{2} = v^{2} \end{matrix}

(14)

összefüggéssel. A (12)‐(14) egyenletrendszert megoldva a tömegek aránya meghatározható,

\begin{matrix} M / m = 7 / 5. \end{matrix}

Czuczor Judit (Paks, Vak Bottyán J. Gimn., III. o. t.)