|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladat egy olyan kúpingára vonatkozik (l. az 1552. feladat KML 59 [1979] 227. o.), amelyre a nehézségi erőn kívül még a töltések vonzásból eredő erő is hat.
Írjuk fel a II. Newton-axióma alapján az tömegi test mozgásegyenletét. Az 1. ábra jelöléseivel az egyenlet és komponensei (-vel a centripetális gyorsulást jelöljük):
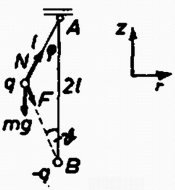 1. ábra 1. ábra
Kifejezhetjük szögfüggvényeit -vel: | |
A Coulomb-törvény szerint Ezek felhasználásával (1)-ből -t kifejezzük, és behelyettesítjük (2)-be: | |
A centeripetális gyorsulást ismerjük:
ezt az egyeletbe behelyettesítve átrendezés után | | (3) |
adódik.
Az és értékekkel:
A keringési idő .
A legkisebb értéket a egyenlet felhasználásával kaphatnánk. Így magasabb fokú egyenletet kapunk, ezért annak egzakt megoldása helyett a minimumot numerikusan keressük.
 2. ábra 2. ábra
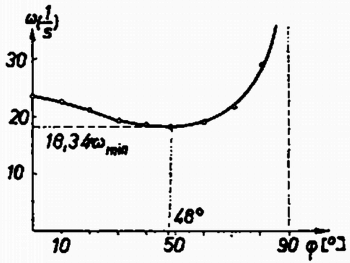
Az egyes értékeket a következő táblázat rögzíti, a görbe menetét a 2. ábrán láthatjuk.
Így azt kapjuk, hogy a legkisebb szögsebesség ωmin=18,341/s, a hozzá tartozó szög φ0≈48∘.
Borbély Gábor (Kapuvár, Gimn., IV. o. t.)
Megjegyzések. 1. A valóságban rögzített φ-nél az erőtörvényekből és a mozgásegyenletből számolt szögsebességgel nem mindig jön létre körmozgás, meg kell vizsgálni a pályamozgás stabilitását. Ha q=0, akkor nyilvánvalónak tűnik a stabilitás. Kicsiny sugárirányú lökést adunk a golyónak, akkor ez az impulzusmomentum megmaradása miatt nagyobb szögsebességgel indul el egy olyan beljebb levő pályán, amelyhez még az előző szögsebességénél is kisebb ω tartozik, ezért a golyó visszatér az eredeti pályája felé. q≠0 esetén részletesebben meg kell vizsgálnunk a kérdést.
A kis Δφ elmozdulásokkal szembeni stabilitás feltételét keressük. Az impulzusmomentum z komponense megmaradó mennyiség: Ezt az összefüggést a szorzat deriválási szabálya alapján φ szerint deriválva kapjuk: | ml2[ω(dω/dφ)sin2φ+ω⋅2sinφcosφ]=0, |
ebből Tehát a kicsiny Δφ kimozdulás esetén a test szögsebességének változása
A körmozgás stabil a Δφ elfordulással szemben, ha a φ+Δφ pályához tartozó szögsebesség (ezt a (3) kifejezéssel számíthatjuk ki) Δφ>0 esetén nagyobb, mint ω+Δω (az a szögsebesség, amelyet a test a kimozdulás során felvesz). Ekkor ugyanis kisebb szögsebességgel indulna el egy nagyobb szögsebességhez tartozó pályán, így a Coulomb- és a kötélerő visszahúzná. Ugyanígy az is szükséges, hogy egy Δφ<0 elmozdulásra ω+Δω nagyobb legyen, mint amekkora szögsebességet a centripetális erő biztosítani tud, ekkor ugyanis a test visszalendül az eredeti helyzete felé. A stabilitás feltétele tehát az, hogy az ω(φ) görbe meredeksége mindig nagyobb legyen, mint ‐ 2ωctg φ.
A (3)-ból adódó ω(φ) függvény legkisebb meredeksége közelítőleg
(1/10∘)[φ(40∘)-φ(30∘)]=-0,11/∘s, ez jóval nagyobb, mint ‐ 2ωctgφ értéke, pl. ha 0≤φ≤89∘,90∘ közelében viszont ω(φ) meredeksége pozitív, míg ‐ 2ωctgφ negatív. A stabilitás feltétele tehát teljesül minden helyzetben.
2. Az (1)-(2) egyenletrendszer csak akkor határozza meg a mozgást, ha a q töltés gyorsulásából eredő sugárzási veszteség elhanyagolható, vagyis amíg a frekvencia elegendően kicsi. |
|
 PDF |
PDF |  MathML
MathML 
