Kezdőlap


Feladat:	1578. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bene Gyula , Csordás András , Horváth István , Kaufmann Zoltán , Pöltl János Tamás , Umann Gábor , Várhelyi Tamás
Füzet:	1980/március, 131 - 132. oldal		PDF \| MathML
Témakör(ök):	Rezgőmozgás (Tömegpont mozgásegyenlete), Newton-féle gravitációs erő, Egyéb erőtörvény, Coulomb-törvény, Energiamegmaradás tétele, Feladat
Hivatkozás(ok):	Feladatok: 1979/április: 1578. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A golyó teljes energiája az elektrosztatikus és a rugalmas helyzeti energia és a mozgási energia összege:

\begin{matrix} E = E_{h} + E_{m} = k \frac{q Q}{a - x} + \frac{1}{2} D x^{2} + \frac{1}{2} m v^{2} . \end{matrix}

(1)

(

Q

és

q

ellentétes előjelű, így

q Q < 0

Ábrázoljuk vázlatosan a helyzeti energiát a golyó helyzete függvényében! A golyó a helyi minimum környezetében végezhet rezgéseket. Adott

E

teljes energia esetén a rezgés azon a szakaszon történhet, ahol

E_{h} \leq E

, tehát a mozgási energiára nemnegatív érték adódik. A legnagyobb amplitúdójú rezgés szélső pontjai

A

és

B

, a teljes energia ekkor a helyzeti energia helyi maximumának

E_{0}

értékével egyenlő.
1. Vizsgáljuk meg először, hogy a paraméterek milyen választása mellett jöhet létre egyáltalán rezgés! A golyóra ható erő két pontban, a helyzeti energia maximumánál

(B)

és az egyensúlyi helyzetben

(C)

nullával egyenlő (l. az ábrát).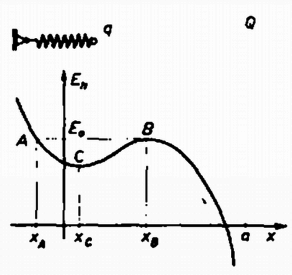

\begin{matrix} F = - \frac{d E_{h}}{d x} = - \frac{k q Q}{{(a - x)}^{2}} - D x = 0, \end{matrix}

(2)

ahonnan

\begin{matrix} D x {(a - x)}^{2} + k q Q = 0, & (3) \\ D x^{3} - 2 D a x^{2} + D a^{2} x + k q Q = 0. & (3') \end{matrix}

D

-t csökkentjük, a helyzeti energiát egyre inkább az elektrosztatikus energia határozza meg, kis

D

-k esetén

(D \leq D_{0})

a minimum eltűnik. Határesetben a

(3)

egyenlet a

B

és

C

ponthoz tartozó megoldása egybeesik, tehát a hozzátartozó gyöktényező az egyenlet gyöktényezős alakjában kétszer fordul elő! Ennek következtében ez a gyök a bal oldal deriváltjának is gyöke:

\begin{matrix} 3 D x^{2} - 4 D a x + D a^{2} = 0. \end{matrix}

(4)

Ez az egyenlet már csak másodfokú, a fizikailag lényeges gyöke

a / 3

. (A második gyök

a

.) Ha tehát

D

egy értéke mellett

B

és

C

egy pontba esik, ez a pont

x = a / 3

-nál van. A

(3)

egyenletbe helyettesítve

D_{0}

meghatározható:

\begin{matrix} D_{0} = - \frac{27}{4} \cdot \frac{k q Q}{a^{3}} . \end{matrix}

(5)

Rezgés csak akkor jöhet létre, ha

D > D_{0}

.
A további számítások során harmadfokú egyenletek megoldására lesz szükség. Ez ugyan általános esetben is megtehető, azonban az összefüggések annyira bonyolulttá válnak, hogy taglalásuk gyakorlatilag lehetetlen. Ezért ezután csak azzal a speciális esettel foglalkozunk, amikor

D = 2 D_{0}

.
2. Határozzuk meg a maximális amplitúdójú rezgés nyugalmi helyzetét és szélső pontjait! A

B

és

C

pontban a golyóra ható erők eredője nulla. A

(3)

egyenletben

D

helyére

2 D_{0}

-at helyettesítve és az

x = y + (2 a / 3)

új ismeretlent bevezetve

\begin{matrix} y^{3} - (a^{2} / 3) y = 0. \end{matrix}

(6)

Az egyenlet három gyöke közül

y_{B} = 0

x_{B} = 2 a / 3

Q

töltéshez közeli szélső pontot határozza meg.

y = a (\sqrt[]{3} / 3)

esetén

x > a

, ez fizikailag értelmetlen gyök.

y_{C} = - a (\sqrt[]{3} / 3)

x_{C} = a (2 - \sqrt[]{3}) / 3

a rezgés nyugalmi helyzetét adja.
A rezgés teljes energiájára

x_{B}

-t

(1)

-be helyettesítve

E_{0} = 0

adódik.

E > 0

esetén a golyó a

Q

töltésbe zuhan,

E (x_{C}) < E \leq E_{0} = 0

esetén rezgés alakul ki. A helyzeti energia a másik szélső helyzetben is

E_{0} = 0

, így

(1)

-ből

x_{A}

-ra harmadfokú egyenlet adódik. Ennek az egyenletnek

x_{B}

is (kétszeres) gyöke, így

x_{B}

gyöktényezőjével osztva az egyenlet fokszáma redukálható és

x_{A}

könnyen meghatározható,

x_{A} = - a / 3

.
A rezgés teljes amplitúdója tehát

x_{B} - x_{A} = a

, nyugalmi helyzete

x_{C} = a (2 - \sqrt[]{3}) / 3

.
A legnagyobb energiájú "rezgés'' tehát tulajdonképpen nem rezgés, mivel a

B

pontban levő labilis egyensúlyi helyzetet a golyó egyre csökkenő sebességgel végtelen hosszú idő alatt éri el.

E_{0}

-nál akármilyen kis értékkel kisebb energiák esetén a rezgésidő természetesen véges.
3. Érdemes meghatározni a nagyon kis amplitúdójú rezgések rezgésidejét. A mozgás ekkor jó közelítéssel harmonikus rezgőmozgásnak tekinthető. Ugyanis az

y

kitérést

x_{C}

-től számítva a visszatérítő erő

(2)

alapján:

\begin{matrix} F = - \frac{k q Q}{{(a - y - x_{C})}^{2}} - D (y + x_{C}) = - \frac{k q Q}{{[(a - x_{C}) - y]}^{2}} - D (y + x_{C}) \approx \\ \approx - \frac{k q Q}{{(a - x_{C})}^{2} - 2 (a - x_{C}) y} - D (y + x_{C}) = - \frac{k q Q}{{(a - x_{C})}^{2}} [\frac{1}{1 - \frac{2 y}{a - x_{C}}}] - D (y + x_{C}) \approx \\ \approx - \frac{k q Q}{{(a - x_{C})}^{2}} (1 + \frac{2 y}{a - x_{C}}) - D (y + x_{C}) = - \frac{k q Q}{{(a - x_{C})}^{2}} - D x_{C} - [\frac{2 k q Q}{{(a - x_{C})}^{3}} + D] y . \end{matrix}

Az első két tag összege

(2)

alapján

0

, hiszen

x_{C}

az egyensúlyi helyzet. Így a visszatérítő erő közelítőleg

y

-nal arányos, az arányossági tényező

\begin{matrix} D^{*} = D + \frac{2 k q Q}{{(a - x_{C})}^{3}}, \end{matrix}

D = 2 D_{0}

speciális esetben

\begin{matrix} D^{*} = \frac{2 k q Q}{a^{3}} {(\frac{3}{1 + \sqrt[]{3}})}^{3} + D = - \frac{27 k q Q}{2 a^{3}} (6 - 3 \sqrt[]{3}) . \end{matrix}

A kis amplitúdójú rezgések rezgésideje tehát

\begin{matrix} T = 2 π \sqrt[]{\frac{m}{D^{*}}} . \end{matrix}