Feladat:	1570. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bene Gyula ,  Benkő Zsigmond ,  Csordás András ,  Egyed Károly ,  Kaufmann Zoltán ,  Szalontai Zoltán
Füzet:	1980/február, 86 - 87. oldal		PDF  |  MathML
Témakör(ök):	Gördülés (Merev testek síkmozgása), Tapadó súrlódás, Munkatétel, Feladat
Hivatkozás(ok):	Feladatok: 1979/március: 1570. fizika feladat

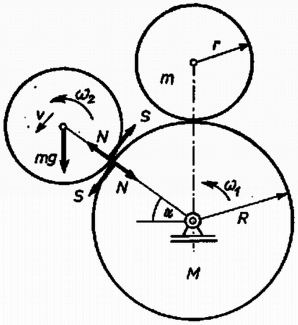
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     Tekintsük azt a megcsúszás előtti helyzetet, amikor a két henger tengelyére illeszkedő sík a vízszintessel $\alpha$ szöget zár be! A nagy henger rögzített tengely körüli forgómozgást végez ${\omega }_1$ szögsebességgel és ${\beta }_1$ szöggyorsulással. A kis henger mozgását bontsuk fel tömegközéppontjának haladó mozgására és a tömegközéppont körüli ${\omega }_2$ szögsebességű, ${\beta }_2$ szöggyorsulású forgómozgásra. A tömegközéppont $v$ sebességű körmozgást végez, érintő irányú gyorsulása $a_t$, centripetális gyorsulása $a_{cp}$. A testekre az ábrán látható erők hatnak.     Írjuk fel a mozgásegyenleteket: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(1/2\right)M{R}^2{\beta }_1=SR\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle \left(1/2\right)m{r}^2{\beta }_2=Sr\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle m{a}_t=mg\text{cos}\alpha -S\mathrm{,}}\hfill & \text{(<mn>3</mn>)}\\ \hfill {\displaystyle m{a}_{cp}=mg\text{sin}\alpha -N\mathrm{.}}\hfill & \text{(<mn>4</mn>)}\end{array}}$ A centripetális gyorsulás: $\begin{array}{c}{\displaystyle a_{cp}=\frac{v^2}{r+R}\mathrm{.}}\end{array}$ (5) A két henger érintkezési pontjának sebessége ugyanakkora, akár a nagy, akár a kis henger pontjának sebességeként fejezzük ki, így ${\displaystyle \begin{array}{cc}\hfill {\displaystyle v-{\omega }_{2}r={\omega }_{1}R\mathrm{,}}\hfill & \text{(<mn>6</mn>)}\\ \hfill {\displaystyle a_t-{\beta }_{2}r={\beta }_{1}R\mathrm{.}}\hfill & \text{(<mn>7</mn>)}\end{array}}$ A súrlódási erő (1), (2), (3) és (7) segítségével meghatározható: $\begin{array}{c}{\displaystyle S=\frac{Mmg\text{cos}\alpha }{3M+2m}\mathrm{.}}\end{array}$ (8) A nyomóerő kifejezéséhez szükségünk van a kis henger sebességére. Ezt a legegyszerűbben az energiamegmaradás tétele segítségével határozhatjuk meg: $\begin{array}{c}{\displaystyle mg\left(R+r\right)\left(1-\text{sin}\alpha \right)=\left(1/2\right)m{v}^2+\left(1/4\right)m{r}^2{\omega }_2^2+\left(1/4\right)M{R}^2{\omega }_1^2\mathrm{.}}\end{array}$ (9) ${\omega }_1$-et és ${\omega }_2$-t $v$-vel kell kifejeznünk. Ehhez egyrészt felhasználjuk a (6) kényszerfeltételt, másrészt (1) és (2) hányadosát képezve $\begin{array}{c}{\displaystyle \frac{{\beta }_1}{{\beta }_2}=\frac{mr}{MR}\mathrm{.}}\end{array}$ Mivel ez az összefüggés a hengerek megmozdulásától kezdve fennáll, a szögsebességekre is érvényes, hogy $\begin{array}{c}{\displaystyle \frac{{\omega }_1}{{\omega }_2}=\frac{mr}{MR}\mathrm{.}}\end{array}$ (10) (9), (6) és (10) felhasználásával $\begin{array}{c}{\displaystyle v^2=\frac{4g\left(R+r\right)\left(1-\text{sin}\alpha \right)\left(m+M\right)}{2m+3M}\mathrm{.}}\end{array}$ (11) (11)-et (5)-be, majd (4)-be helyettesítve a nyomóerő $\begin{array}{c}{\displaystyle N=\frac{mg\left[\text{sin}\alpha \left(7M+6m\right)-4\left(m+M\right)\right]}{3M+2m}\mathrm{.}}\end{array}$ (12) Annak feltétele, hogy a két henger ne csússzék meg egymáson: $\begin{array}{c}{\displaystyle S\le \mu N\mathrm{.}}\end{array}$ (13) Először oldjuk meg az $S\le \mu N$ egyenletet. Tekintve, hogy $0$ és $\pi /2$ között a $\text{sin}$ függvény szigorúan nő, a $\text{cos}$ függvény szigorúan csökken, (8) és (12) alapján világos, hogy $0$ és $\pi /2$ között (az $\alpha$-ra vonatkozó) $S=\mu N$ egyenletnek legfeljebb egy megoldása lehet. (8) és (12) behelyettesítésével, négyzetre emelve a következő egyenletet kapjuk: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{sin}{}^2\alpha \left[{\mu }^2{\left(7M+6m\right)}^2+M^2\right]-\text{sin}\alpha \cdot 8{\mu }^2\left(m+M\right)\left(7M+6m\right)-}\hfill \\ \hfill {\displaystyle -M^2+16{\mu }^2{\left(m+M\right)}^2=0.}\hfill & \text{(<mn>14</mn>)}\end{array}}$ A $\text{sin}\alpha$-ra vonatkozó másodfokú egyenlet két gyöke közül a nagyobbik a számunkra érdekes (a megfelelő hegyesszöget jelölje ${\alpha }_1$): $\begin{array}{c}{\displaystyle \text{sin}{\alpha }_1=\frac{4{\mu }^2\left(m+M\right)\left(7M+6m\right)+M\sqrt[]{M^2+{\mu }^2\left(10m+11M\right)\left(2m+3M\right)}}{{\mu }^2{\left(7M+6m\right)}^2+M^2}\mathrm{,}}\end{array}$ mivel könnyen látható, hogy erre teljesül a $\begin{array}{c}{\displaystyle 0<\text{sin}{\alpha }_1<1}\end{array}$ feltétel, továbbá ezt (12)-be helyettesítve $N$-re pozitív érték adódik, míg a másik gyökre a fenti feltételek mindegyike nem teljesül. (Ez következik abból is, hogy $0$ és $\pi /2$ között az $S=\mu N$ egyenletnek legfeljebb egy megoldása lehet.) Mivel a $\text{sin}$ függvény szigorúan nő, a $\text{cos}$ függvény szigorúan csökken $0$ és $\pi /2$ között, azért (8) és (12) alapján adódik, hogy $\pi /2\ge \alpha \ge {\alpha }_1$ esetén a (13) egyenlőtlenség nem teljesül, de $0<\alpha <{\alpha }_1$ esetén $S<\mu N$, tehát az $\alpha ={\alpha }_1$ szögnél szükségképpen megcsúsznak egymáson a hengerek.   Egyed Károly (Gödöllő, Török I. Gimn., IV. o. t.)