Kezdőlap


Feladat:	1561. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kávássy Lóránd , Kolláth Zoltán , Umann Gábor
Füzet:	1980/január, 38 - 40. oldal		PDF \| MathML
Témakör(ök):	Forgási energia, Egyéb merev test síkmozgások, Pillanatnyi forgástengely, Feladat
Hivatkozás(ok):	Feladatok: 1979/február: 1561. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Elegendő, ha csak a létra egyik szárának mozgását vizsgáljuk. Az $l$ hosszú szárra az 1. ábrán feltüntetett erők hatnak. A talaj $N_{1}$ nyomóereje függőleges irányú, mert a súrlódás elhanyagolható, a másik szár által közvetített $N_{2}$ erő pedig a létra szimmetriája miatt csak vízszintes irányú lehet.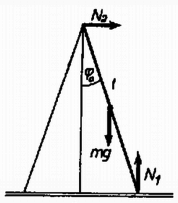

1. ábra

Legyen a szár szöggyorsulása

β

, a tömegközéppont gyorsulásának komponensei legyenek

a_{x}

és

a_{y}

. Írjuk fel a mozgásegyenleteket a tömegközéppontra:

\begin{matrix} m g - N_{1} = m a_{y}, & (1) \\ N_{2} = m a_{x}, & (2) \\ N_{1} (l / 2) sin φ - N_{2} (l / 2) cos φ = Θ_{S} β, & (3) \end{matrix}

ahol a tömegközéppontra vonatkoztatott tehetetlenségi nyomaték:

\begin{matrix} Θ_{S} = (1 / 12) {m l}^{2} . \end{matrix}

(4)

2. ábra

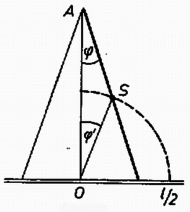A következő lépés a gyorsulás komponensei és a szöggyorsulás közti kapcsolat meghatározása. Vegyük észre, hogy az

S

tömegközéppont az

O

pont körül egy

l / 2

sugarú körön mozog (2. ábra), mégpedig éppen azzal a

β

szöggyorsulással, mint a létra szára az

S

tömegközéppont körül. Az

O S A

háromszög ugyanis egyenlőszárú, ezért

φ (t) = φ' (t)

minden időpillanatban, így második deriváltjuk, a szöggyorsulás is megegyezik. Így

a_{x}

és

a_{y}

a tömegközéppont

O

körüli körmozgásának kerületi gyorsuláskomponensei:

\begin{matrix} a_{x} = β (l / 2) cos φ, & (5) \\ a_{y} = β (l / 2) sin φ . & (6) \end{matrix}

A létra legfelső pontjának elmozdulása mindig kétszerese a súlypont függőleges elmozdulásának, ezért gyorsulása

\begin{matrix} a = 2 a_{y} . \end{matrix}

(7)

Az (1)‐(7) egyenletrendszer megoldása:

\begin{matrix} a = (3 / 2) g sin^{2} φ . \end{matrix}

(8)

t

sokkal kisebb, mint a létra tetejének földet éréséhez szükséges idő, akkor ezalatt

φ

nem sokat változik, és a gyorsulás közel állandónak tekinthető. (8) alapján az igen rövid idő alatt megtett út:

\begin{matrix} s = (1 / 2) {a t}^{2} = (3 / 4) {g t}^{2} sin^{2} φ_{0}, \end{matrix}

vagy

φ_{0} = 15^{\circ}

behelyettesítésével:

\begin{matrix} s = 0, 5 ({m/s}^{2}) \cdot t^{2}, \end{matrix}

Kávássy Lóránd (Kecskemét, Katona J. Gimn., III. o. t.)

II. megoldás. A forgómozgás egyenletét a tömegközépponton kívül a pillanatnyi forgástengelyre is fel tehet írni. A létra szára a 3. ábrán feltüntetett

P

pont körül fordul el. (

P

a szár végpontjainak elmozdulására merőlegesen állított egyenesek metszéspontja.) A

P

pont természetesen ,,vándorol'' a mozgás során. A pillanatnyi forgástengelyre vonatkoztatva a létra szára csak forgómozgást végez:

\begin{matrix} M = Θ β, \\ (1 / 2) m g l sin φ = Θ β . & (9) \end{matrix}

Felhasználtuk, hogy az

N_{1}

és

N_{2}

erők hatásvonala keresztülhalad

P

ponton, így nincs forgatónyomatékuk.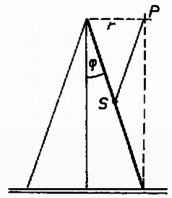

3. ábra

A pillanatnyi forgástengelyre vonatkoztatott tehetetlenségi nyomaték a Steiner-tétel alapján:

\begin{matrix} Θ = Θ_{s} + m {(l / 2)}^{2} = (1 / 3) {m l}^{2} . \end{matrix}

(10)

A felső végpont gyorsulása (l. a 3. ábrát)

\begin{matrix} a = r β = B l sin φ . \end{matrix}

(9) és (10) behelyettesítésével

\begin{matrix} a = (3 / 2) g {sin}^{2} φ . \end{matrix}

A rövid idő alatti elmozdulás az előző megoldással egyezően így

\begin{matrix} s = (3 / 4) {g t}^{2} {sin}^{2} φ_{0} . \end{matrix}

Kolláth Zoltán (Törökszentmiklós, Bercsényi M. Gimn., III. o. t.)

III. megoldás. Alkalmazzuk az energiamegmaradás tételét! Ismét elegendő a létra egyik szárát vizsgálni. Ha a létra teteje

s

utat tesz meg, szárának tömegközéppontja

(s / 2)

-vel kerül lejjebb. A potenciális energia változása

\begin{matrix} Δ U_{p o t} = m g s / 2, \end{matrix}

(11)

a mozgási energia növekedése

\begin{matrix} Δ U_{k i n} = / (1 / 2) Θ_{S} ω^{2} + (1 / 2) {m v}^{2} . \end{matrix}

(12)

Az első megoldásban a kényszerfeltétel keresésekor bizonyítottuk, hogy az

S

tömegközéppont

O

pont körüli forgómozgását ugyanaz a

φ (t)

függvény írja le, mint ami a létra szárának súlypont körüli elfordulását. Emiatt

\begin{matrix} v = (l / 2) ω . \end{matrix}

(13)

Az energiamegmaradás törvénye alapján

Δ U_{p o t} = Δ U_{k i n}

\begin{matrix} (1 / 2) m g s = (1 / 2) \cdot (1 / 3) m {(l / 2)}^{2} ω^{2} + (1 / 2) {m v}^{2}, \end{matrix}

ahonnan

(13)

felhasználásával

\begin{matrix} v = \sqrt[]{(3 / 4) g s} . \end{matrix}

(14)

A súlypont elmozdulásának függőleges sebességkomponense:

v_{y} = sin φ

, a létra csúcsának sebessége pedig

s

út megtétele után:

\begin{matrix} v_{A} = 2 v_{y} = 2 v sin φ = \sqrt[]{3 g s} sin φ . \end{matrix}

(15)

t

sokkal kisebb, mint a földetéréshez szükséges idő, ezért a legfelső pont gyorsulását ezalatt állandónak tekinthetjük. Egyenletesen gyorsuló mozgásnál

\begin{matrix} s = \frac{v_{A} t}{2}, \end{matrix}

azaz (15) alapján

\begin{matrix} s = \frac{\sqrt[]{3 g s}}{2} t sin φ_{0}, így s = (3 / 4) {g t}^{2} {sin}^{2} φ_{0} . \end{matrix}

Umann Gábor (Budapest, Fazekas M. Gyak. Gimn., III. o. t.)