Kezdőlap


Feladat:	1542. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kávássy Lóránd , Madi Tibor , Mihály György , Pálinkás István
Füzet:	1979/november, 168 - 173. oldal		PDF \| MathML
Témakör(ök):	Erők forgatónyomatéka, Párhuzamos erők eredője, Gördülés lejtőn, Feladat
Hivatkozás(ok):	Feladatok: 1978/december: 1542. fizika feladat

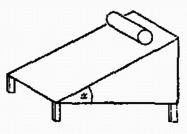
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel a lejtő nincs kitámasztva, és a talaj mentén a súrlódás elhanyagolható, a lejtő is mozogni fog. A lábaknál ható erők megadásához két adat szükséges: a henger lejtőhöz viszonyított helyzete az idő függvényében, valamint a lejtőre ható erő a henger érintkezési pontjánál. Az 1. ábrán a henger lejtőhöz viszonyított helyzetét az $x'$ , $y'$ koordinátákkal; a lejtőre gyakorolt erőt a $K_{x}$ , $K_{y}$ komponensekkel jelöltük.

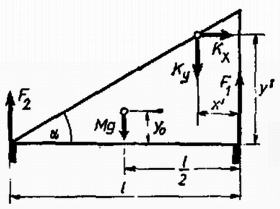1. ábra

A lejtő függőlegesen nem gyorsul, tehát

\begin{matrix} M g + K_{y} = F_{1} + F_{2}, \end{matrix}

(1)

ahol

F_{1}

a magas oldalon,

F_{2}

az alacsony oldalon levő lábaknál ható erők eredője. A lejtő nem fordul el, ezért a tömegközéppontra felírt forgatónyomatékok eredője nulla. (Mivel a lejtő vízszintesen gyorsul, a forgatónyomatékokat nem lehet önkényesen megválasztott pontra felírni. Merev testeknél a tömegközéppontra felírt forgatónyomaték tetszőleges mozgásnál helyes eredményt ad ‐ 1. Budó: Mechanika 28.§ és 49.§.) Ha a lejtő tömegközéppontja

y_{0}

magasságban van ‐ az

l

hosszúságú alaplap mentén középen ‐, akkor a forgatónyomatékok eredője:

\begin{matrix} (l / 2) F_{2} + K_{x} (y' - y_{0}) + K_{y} [(l / 2) - x'] - (l / 2) F_{1} = 0. \end{matrix}

(2)

Az (1) és (2) egyenletekből a lejtő magas oldalán levő egy-egy lábnál ébredő erő:

\begin{matrix} \frac{1}{2} F_{1} = \frac{1}{4} M g + \frac{1}{2} K_{x} \frac{y' - y_{0}}{l} + \frac{1}{2} K_{y} \frac{l - x'}{l}, \end{matrix}

(3)

míg a másik oldalon

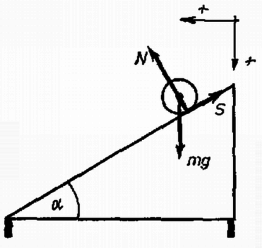\begin{matrix} \frac{1}{2} F_{2} = \frac{1}{4} M g - \frac{1}{2} K_{x} \frac{y' - y_{0}}{l} + \frac{1}{2} K_{y} \frac{x'}{l} . \end{matrix}

(4)

2. ábra

Az erők és a gyorsulások meghatározásához vizsgáljuk először a henger mozgását. A 2. ábrán a hengerre ható erők és a gyorsulásoknál használt pozitív irányok vannak feltüntetve. A lejtő nyomóereje merőleges a lejtő síkjára (tehát

N_{x} = N sin α

N_{y} = N cos α)

, viszont

| N | \neq m g cos α

, mert álló koordináta-rendszerben a henger lejtőirányú elmozdulása a lejtő mozgása miatt azt jelentené, hogy a henger elhagyja a lejtőt.
A mozgásegyenletek:

\begin{matrix} m a_{x} & = N_{x} - S_{x} = N sin α - S cos α, & (5) \\ m a_{y} & = m g - N_{y} - S_{y} = m g - N cos α - S sin α, & (6) \\ Θ β & = (1 / 2) m r^{2} β = S r . & (7) \end{matrix}

Ha a henger csúszva gördül, akkor a súrlódási erő:

\begin{matrix} S = μ N, \end{matrix}

(8)

míg tökéletes gördülésnél

S < μ N

, és ekkor a súrlódási erő értékét a gördülés kényszerfeltételéből lehet meghatározni.

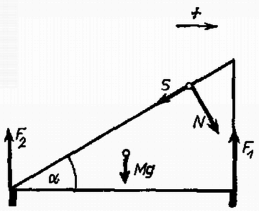3. ábra

A hengerre ható erők ellenereje a 3. ábrán látható. A lejtő vízszintes gyorsulását

(A_{x})

az ábrán feltüntetett előjellel tekintjük pozitívnak. A lejtőre ható erők a henger érintkezési pontjánál:

\begin{matrix} K_{x} = N_{x} - S_{x} = N sin α - S cos α, & (9) \\ K_{y} = N_{y} + S_{y} = N cos α + S sin α . & (10) \end{matrix}

A mozgásegyenlet:

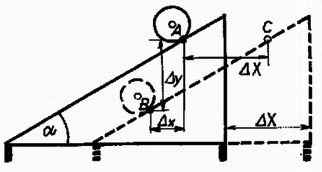\begin{matrix} M A_{x} = N_{x} - S_{x} = N sin α - S cos α . \end{matrix}

(11)

4. ábra

A kényszerfeltételek meghatározásához a 4. ábrán felrajzoltuk a henger és a lejtő helyzetét két egymást követő pillanatban. Mivel a henger a lejtőn marad,

Δ y = (Δ x + Δ X) tg α

, ezt az összefüggést az idő szerint kétszer deriválva az

\begin{matrix} a_{y} = (a_{x} + A_{x}) tg α \end{matrix}

(12)

kényszerfeltételt kapjuk. Tökéletes gördülésnél, ha a henger a két helyzet között

Δ φ

szögelfordulást végez, a henger kerületének

r φ

szakasza megegyezik a

C B

távolsággal (a

C

pontnak megfelelő helyről indult és a

B

pontba érkezett)

\begin{matrix} r φ = \frac{Δ x + Δ X}{cos α}; \end{matrix}

ebből kétszeri deriválással:

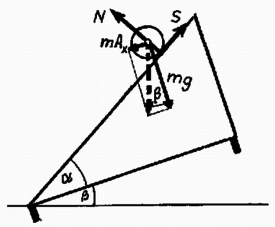\begin{matrix} r β = \frac{a_{x} + A_{x}}{cos α} . \end{matrix}

(13)

5. ábra

Néhány átrendezést meg lehet tenni a csúszva gördülés és a tisztán gördülés esetének szétválasztása előtt. A (6) és (11) egyenlet összehasonlításából:

\begin{matrix} A_{x} = \frac{m}{M} a_{x}, \end{matrix}

(14)

így a ,,lejtőn maradás'' kényszerfeltétele (12) alapján

\begin{matrix} a_{y} = a_{x} [1 + (m / M)] tg α . \end{matrix}

(15)

Csúszás esetén az (5), (6), (8) és (15) egyenletek egyszerű egyenletrendszert alkotnak, amelynek megoldása:

\begin{matrix} a_{x} = \frac{g (sin α - μ cos α) cos α}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)}, & (16) \\ N = \frac{m g cos α}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)} . & (17) \end{matrix}

(Vegyük észre, hogy

M ≫ m

esetén valóban visszakapjuk az álló lejtőnél várt eredményt.)
A henger lejtőhöz viszonyított helyzetének meghatározásához az

x' = (1 / 2) (a_{x} + A_{x}) t^{2}

relatív elmozdulást a (14), az

y' = l sin α - (1 / 2) a_{y} t^{2}

távolságot a (15), a lejtőre ható erőket a (8) és a (9), (10) egyenletekbe való egyszerű behelyettesítéssel kapjuk:

\begin{matrix} x' = & \frac{1}{2} \cdot \frac{g t^{2} (sin α - μ cos α) cos α}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)} [1 + (m / M)], \\ y' & = l sin α - x' tg α, \\ K_{x} & = \frac{m g (sin α - μ cos α) cos α}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)}, \\ K_{y} & = \frac{m g (cos α + μ sin α) cos α}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)} . \end{matrix}

A lejtő lábainál ható erők ezek ismeretében, (3) és (4) alapján:

\begin{matrix} \frac{1}{2} F_{1} = \frac{1}{4} M g + \frac{1}{2} \frac{m g cos α}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)} \cdot \\ \cdot {(sin α - μ cos α) [sin α - \frac{[g t^{2} / (2 l)] (sin α - μ cos α) sin α [1 + (m / M)]}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)} - \frac{y_{0}}{l}] + \\ + (cos α + μ sin α) [1 - \frac{[g t^{2} / (2 l)] (sin α - μ cos α) cos α [1 + (m / M)]}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)}]}, & (18) \\ \frac{1}{2} F_{2} = \frac{1}{4} M g + \frac{1}{2} \frac{m g cos α}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)} \cdot \\ \cdot {(μ cos α - sin α) [sin α - \frac{[g t^{2} / (2 l)] (sin α - μ cos α) sin α [1 + (m / M)]}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)} - \frac{y_{0}}{l}] + \\ + (cos α - μ sin α) \frac{[g t^{2} / (2 l)] (sin α - μ cos α) cos α [1 + (m / M)]}{1 + (m / M) - (m / M) cos α (cos α + μ sin α)}} . & (19) \end{matrix}

Tökéletes gördülésnél a súrlódási erőt a (

8

) egyenlet helyett a (

1

) kényszerfeltételből és a forgómozgást leíró (

7

) egyenletből kell meghatározni:

\begin{matrix} S = \frac{1}{2} m \frac{a_{x} + A_{x}}{cos α} = \frac{1}{2} \frac{m a_{x}}{cos α} (1 + \frac{m}{M}) . & (20) \end{matrix}

A csúszásmentesen gördülő henger mozgását leíró

(5)

(6)

(15)

és

(20)

egyenletek megoldása:

\begin{matrix} a_{x} = \frac{(2 / 3) g sin α cos α}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α}; & (21) \\ a_{y} = \frac{(2 / 3) g sin^{2} α [1 + (m / M)]}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α}; & (22) \\ S = \frac{1}{3} \frac{m g sin α [1 + (m / M)]}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α}; & (23) \\ N = (1 + \frac{m}{3 M}) \frac{m g cos α}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α} . & (24) \end{matrix}

x'

y'

koordináták, valamint

K_{x}

és

K_{y}

meghatározása

a_{x}

a_{y}

S

és

N

ismeretében ugyanúgy történik, mint az előbb. Ha ezeket kiszámoltuk,

(3)

-ba és

(4)

-be helyettesítve tisztán gördülés esetén a végeredmény:

\begin{matrix} \frac{1}{2} F_{1} = \frac{1}{4} M g + \frac{1}{3} \cdot \frac{m g sin α cos α}{1 + (m / M) - (2 / 3) (M / m) cos^{2} α} \cdot \\ \cdot {sin α - \frac{1}{3 l} \cdot \frac{g t^{2} sin^{2} α [1 + (m / M)]}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α} - \frac{y_{0}}{l} + [\frac{3}{2} (1 + \frac{m}{3 M}) ctg α + \frac{1}{2} (1 + \frac{m}{M}) tg α] \cdot \\ \cdot (1 - \frac{1}{3 l} \frac{g t^{2} sin α cos α}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α})}; & (25) \\ \frac{1}{2} F_{2} = \frac{1}{4} M g + \frac{1}{3} \frac{m g sin α cos α}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α} \cdot \\ \cdot {\frac{1}{3 l} \frac{g t^{2} sin^{2} α [1 + (m / M)]}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α} + \frac{y_{0}}{l} - sin α + \\ + [\frac{3}{2} (1 + \frac{m}{3 M}) ctg α + \frac{1}{2} (1 + \frac{m}{M}) tg α] \frac{1}{3 l} \frac{g t^{2} sin α cos α}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α}} . (26) \end{matrix}

Tökéletes gördülés akkor jön létre, ha a súrlódási együttható egy kritikus,

μ_{0}

értéknél nagyobb. A kritikus súrlódási együtthatót legegyszerűbben abból a feltételből határozhatjuk meg, hogy ha

μ = μ_{0}

, akkor a ,,csúszva gördüléshez'' és a tökéletes gördüléshez tartozó gyorsulásértékek megegyeznek.

(16)

és

(21)

egyenlővé tételével

μ_{0}

-ra egyenletet kapunk, aminek megoldása:

\begin{matrix} μ_{0} = \frac{1}{3} tg α \frac{1 + (m / M)}{1 + [m / (3 M)]} . \end{matrix}

(27)

Mint minden korábbi kifejezés, ez is visszaadja a várt eredményt

M ≫ m

esetén.
Összefoglalva: a lejtő lábánál fellépő erők az idő függvényében olyan parabolaívekkel ábrázolhatók, amelyek paramétereit a

μ \leq μ_{0}

esetben a

(18)

(19)

; a

μ \geq μ_{0}

esetben a

(25)

(26)

egyenletek adják meg.

II. megoldás. Az előző megoldás hosszadalmas (elsősorban a sokismeretlenes egyenletrendszerek megoldása miatt), azonban kellő türelemmel különösebb nehézség nélkül végigszámolható. Az alábbi megoldásban ‐ ahol a lejtővel együtt gyorsuló koordináta-rendszerben számolunk ‐ a számolási munka lényegesen kevesebb, de több buktatóval találkozhatunk.
A gyorsuló koordináta-rendszerre vonatkozó mennyiségeket

'

-vel jelöljük. A hatás‐ellenhatás törvénye alapján tudjuk, hogy álló rendszerben

m a_{x} = M A_{x}

, azaz a lejtővel együtt gyorsuló rendszerben a henger gyorsulása:

\begin{matrix} a'_{x} = a_{x} + A_{x} = [(M / m) + 1] A_{x} . \end{matrix}

(1)

A gyorsuló koordináta-rendszer nem inerciarendszer, de az ún. tehetetlenségi erők bevezetésével alkalmazhatók a Newton-törvények. (Gyorsuló rendszerről 1.: Budó ‐ Pócza: Kísérleti Fizika I. rész. F. fejezet.) Az

A_{x}

gyorsulással mozgó rendszerben a

m

tömegű hengerre

- m A_{x}

, a lejtőre

- M A_{x}

tehetetlenségi erő hat, amelyek támadáspontja az egyes testek tömegközéppontja. A gyorsuló koordináta-rendszerben a hengerre ható erők az 5. ábrán láthatók. Az ábra alapján megállapíthatjuk, hogy a henger úgy fog mozogni, mintha egy

α' = α + β

hajlásszögű lejtőn

g' = g / cos β

nehézségi gyorsulású térben lenne, ahol

\begin{matrix} tg β = A_{x} / g . \end{matrix}

(2)

A közismert eredmények felhasználásával, csúszásnál

\begin{matrix} a' = g' (sin α' - μ cos α'), \end{matrix}

(3a)

illetve tökéletes gördülésnél

\begin{matrix} a' = (2 / 3) g' sin α' \end{matrix}

(3b)

a henger lejtő irányú gyorsulása. Az alaplappal párhuzamos komponens mindkét esetben:

a'_{x} = a' cos α

. Az

α' = α + β

és

g' = g / cos β

behelyettesítésével:

\begin{matrix} a'_{x} = g cos α [sin α - μ cos α + tg β (cos α + μ sin α)], \end{matrix}

(4a)

illetve

\begin{matrix} a'_{x} = (2 / 3) g cos α (sin α + tg β cos α) . \end{matrix}

(4b)

(1)

és

(2)

alapján

tg β = \frac{a'_{x}}{(M / m) + 1}

. Ezt a fenti kifejezésekbe behelyettesítve egyismeretlenes egyenletet kapunk

a'_{x}

-re. A megoldás:

\begin{matrix} a'_{x} = \frac{g (sin α - μ cos α) cos α [1 + (m / M)]}{1 + (m / M) - (m / M) cos α + μ sin α)}, \end{matrix}

(5a)

illetve

\begin{matrix} a'_{x} = \frac{(2 / 3) g sin α cos α [1 + (m / M)]}{1 + (m / M) - (2 / 3) (m / M) cos^{2} α} \end{matrix}

(5b)

(valóban megegyezik az I. megoldás

a_{x} + A_{x} = [1 + (m / M)] a_{x}

értékével). A függőleges komponens mindkét esetben

a'_{y} = a'_{x} tg α

.
A lejtőre a hengerre ható erők ellenereje hat. Mivel a henger vízszintes gyorsulása

a'_{x}

;

| K_{x} | = m a'_{x}

, és mivel a függőleges gyorsulása

a'_{y}

;

| K_{y} | = m (g - a'_{y}) = m (g - a'_{x} tg α)

. A lábaknál ható erők meghatározásához felírandó egyenletek ugyanazok, mint az első megoldás

(1) - (2)

egyenletei. (Ha nem feledkezünk meg a gyorsuló koordináta-rendszerben a lejtő tömegközéppontjában ható

- M A_{x}

tehetetlenségi erőről, akkor ebben a rendszerben a forgatónyomaték már tetszőleges pontra felírható.)
Az eredményben szereplő mennyiségek (

K_{x}

K_{y}

x' = (1 / 2) a'_{x} t^{2}

és

y' = l sin α - (1 / 2) a'_{x} tg α \cdot t^{2}

) csak

a'_{x}

-t tartalmazzák paraméterként, amit a csúszás, illetve a gördülés esetére az

(5)

egyenletben már kiszámoltunk. A helyettesítés után kapott eredmény természetesen megegyezik az I. megoldás végeredményével.

Mihály György