Feladat: 1534. fizika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Pálinkás István 
Füzet: 1979/szeptember, 38 - 40. oldal  PDF  |  MathML 
Témakör(ök): Erők forgatónyomatéka, Párhuzamos erők eredője, Gördülés lejtőn, Függvények grafikus elemzése, Feladat
Hivatkozás(ok):Feladatok: 1978/november: 1534. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A lejtőn guruló hengerre az mg súlyerőn kívül a lejtő merőleges nyomóereje (N) és az S súrlódási erő hat (1. ábra).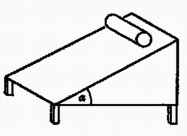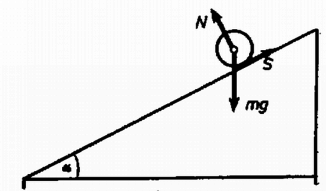

 


 

 
1. ábra

 

Mivel a henger lejtőirányú mozgást végez, e három erő eredőjének lejtőirányúnak kell lennie, azaz
N=mgcosα.(1)
A haladó mozgást leíró egyenlet
mgsinα-S=ma,(2)
míg a középpont körüli forgómozgást az
M=Θβ
azaz
Sr=(1/2)mr2β(3)
összefüggés határozza meg.
A súrlódási együttható értékétől függően két eset lehetséges: a) a henger tisztán gördül, b) a henger csúszva gördül.
Nézzük először az első esetet. Ekkor a haladó mozgás gyorsulása és a forgás szöggyorsulása között meghatározott összefüggés van:
a=rβ.(4)
A (4) kényszerfeltétellel a (2) és (3) egyenletek megoldása:
a=(2/3)gsinα,(5)S=(1/3)mgsinα.(6)

A súrlódási erő így kapott értékének teljesítenie kell az
S≤μN(7)
feltételt. Ha ez igaz, azaz
(1/3)mgsinα≤μmgcosα,(8)
μ≥(1/3)tgα,


akkor a henger tökéletesen gördülve halad végig a lejtőn.
Ennél kisebb súrlódási együtthatók mellett a henger csúszva gördül. Ekkor a (4) kényszerfeltétel nem teljesül. A súrlódási erőről viszont tudjuk, hogy csúszásnál felveszi maximális értékét:
S=μN=μmgcosα,(9)
és a tömegközéppont gyorsulása (2) alapján
a=g(sinα-μcosα).(10)

 

 
2. ábra

 

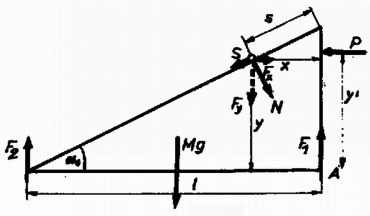Vizsgáljuk a lejtőre ható erőket! Ha a henger középen gördül, a lejtő magasabb, illetve alacsonyabb oldalának két-két lábán ugyanakkora erő hat. Ezek eredőjét jelöljük F1 gyel, ill. F2-vel (2. ábra). A lábaknál ható erők függőleges irányúak, hiszen a "talaj igen sima'' ‐ a súrlódás elhanyagolható.
A henger érintkezési pontjánál a lejtőre a nyomóerő és a súrlódási erő ellenereje hat. Ezek eredőjének függőleges komponense:
Fy=mgcos2α+S1sinα,(11)
vízszintes komponense
Fx=mgcosαsinα-Scosα.(12)
A lejtőre hat még a saját súlya, amelynek nagysága Mg; valamint a magas oldal kitámasztásánál a lejtő elmozdulását megakadályozó P nagyságú erő, aminek támadáspontját jellemezzük az y' magassággal (2. ábra).
A lejtő akkor van egyensúlyban, ha az erők és a forgatónyomatékok eredője nulla. Az erők komponenseire felírható egyenletek:
Mg+Fy=F1+F2,(13)Fx=P.(14)


Jellemezzük a henger helyzetét a 2. ábrán feltüntetett x és y koordinátákkal, majd írjuk fel az A pontra vonatkoztatott forgatónyomatékok eredőjét (a lejtő alapja l hosszú):
Mg(l/2)+Fyx+Py'-F2l-Fxy=0.(15)
A (13), (14) és (15) egyenletek megoldása:
F1=(Mg/2)+Fy[1-(x/l)]+Fx(y-y')/l,(16)F2=(Mg/2)+Fy(x/l)-Fx(y-y')/l.(17)


A feladat kitűzéséből nem egyértelmű, hogy a kitámasztást hogyan végezzük. Az egyszerűség kedvéért tegyük fel, hogy a P erővel mindig a hengerrel egyforma magasságban hatunk. Ekkor a (16) és (17) egyenletek utolsó tagja nulla.
Ha a henger a lejtő tetejéről kezdősebesség nélkül indul, akkor az általa megtett út s=(1/2)at2 és x=scosα.
Ha μ≥(1(3)tgα, a henger tisztán gördül és az (5), (6) összefüggéseket kell alkalmazni. (11) és (12) felhasználásával (16) és (17) alapján a lejtő magas oldalán levő lábaknál fellépő erő:
F1/2=Mg/4+(mg/2)[cos2α+(1/3)sin2α][1-(1/3)(gt2/l)sinαcosα],
míg a másik oldalon
F2/2=(Mg/4)+(mg/2)[cos2α+(1/3)sin2α](1/3)(gt2/l)sinαcosα.

Csúszva gördülésnél [μ<(1/3)tgα] a (9) és (10) összefüggéseket kell behelyettesíteni. Ekkor:

F1/2=(Mg/4)+(mg/2)(cos2α+μcosαsinα)[1-(gt2/l)cosα(sinα-μcosα)];F2/2=(Mg/4)+(mg/2)(cos2α+μcosαsinα)(gt2/l)(sinα-μcosα)cosα.



A 3. ábrán az erőket az idő függvényében ábrázoltuk; F1-et szaggatott, F2-t folytonos vonallal. Valamennyi görbe parabolaív.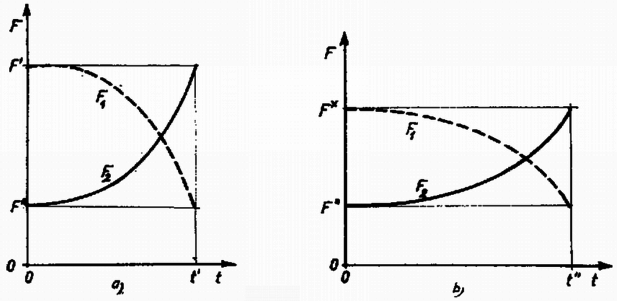
 

 
3. ábra

 

Pálinkás István (Szolnok, Verseghy F. Gimn., III. o. t.)

dolgozata alapján