Feladat:	1516. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Czinege Zoltán
Füzet:	1979/március, 134 - 135. oldal		PDF  |  MathML
Témakör(ök):	Nyomóerő, kötélerő, Körmozgás (Tömegpont mozgásegyenlete), Tömegpont egyensúlya, Centrifugális erő, Feladat
Hivatkozás(ok):	Feladatok: 1978/szeptember: 1516. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.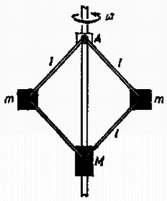     Rajzoljuk be az egyes testekre ható erőket (1. ábra)! A rudakban ható kényszererők a rúd tengelyével párhuzamosak, ellenkező esetben ugyanis forgatónyomatékuk a súlytalan rúd végtelen nagy szöggyorsulását eredményezné. 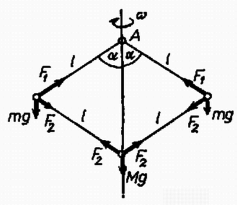    1. ábra   Írjuk fel a mozgásegyenleteket! A $m$ tömegű testek körmozgást végeznek, így vízszintes centripetális gyorsulásuk van. Az erők vízszintes komponenseire vonatkozó mozgásegyenlet: $\begin{array}{c}{\displaystyle F_1\text{sin}\alpha +F_2\text{sin}\alpha =mr{\omega }^2\mathrm{,}}\end{array}$ (1) ahol $\begin{array}{c}{\displaystyle r=l\text{sin}\alpha \mathrm{.}}\end{array}$ (2) Függőlegesen egyik test sem gyorsul, így ${\displaystyle \begin{array}{cc}\hfill {\displaystyle mg+F_2\text{cos}\alpha -F_1\text{cos}\alpha =\mathrm{0,}}\hfill & \text{(<mn>3</mn>)}\\ \hfill {\displaystyle Mg-2F_2\text{cos}\alpha =0.}\hfill & \text{(<mn>4</mn>)}\end{array}}$ Oldjuk meg az egyenletrendszert $\alpha$-ra! (2)-t (1)-be helyettesítve nyilvánvaló, hogy $\text{sin}\alpha =0$, $\alpha =0$ az egyenlet triviális megoldása. Ekkor $F_2=\left(Mg/2\right)$, $F_1=mg+\left(Mg/2\right)$. A rendszer tehát mindig nyugalomban van, ha a rudak nem nyílnak szét, azaz, ha a $M$ tömegű test $A$-tól $2l$  távolságra van. Ha $\text{sin}\alpha \ne 0$, az egyenletrendszer megoldása $\begin{array}{c}{\displaystyle \overline{AM}=2l\text{cos}{\alpha }_0=\frac{2\left(M+m\right)g}{m{\omega }^2}\approx \frac{60{\text{ m/s}}^2}{{\omega }^2}\mathrm{.}}\end{array}$ (5) Érdekes módon az eredmény nem függ $l$-től. A szögsebesség csökkentésével az $AM$ távolság nő, azonban $\overline{AM}\leqq 2l$, ahonnan (5) felhasználásával 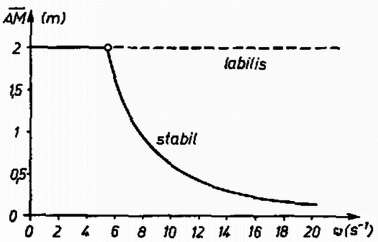$\begin{array}{c}{\displaystyle \omega \ge {\omega }_{\text{min}}=\sqrt[]{\frac{\left(m+M\right)g}{lm}}\approx 5\mathrm{,}5{\text{s}}^{-1}\mathrm{.}}\end{array}$ Kis szögsebesség esetén a rudak nem térnek ki az $\alpha =0$ helyzetből. $\omega \geqq {\omega }_{\text{min}}$ esetén $\alpha =0$ labilis egyensúlyi helyzetté válik, a stabil egyensúlyi helyzetet az (5) összefüggés adja meg (2. ábra).     2. ábra    Czinege Zoltán (Debrecen, KLTE Gyak. Gimn., III. o. t.)   Megjegyzés. Vizsgáljuk meg az egyensúlyi helyzetek stabilitását! Rögzítsük a rendszert egy adott $\alpha$-val jellemzett helyzetben úgy, hogy a $M$ tömegű testet egy függőlegesen lefelé ható $F$  erővel tartjuk. Ekkor a (4) egyenlet így módosul: $\begin{array}{c}{\displaystyle Mg+F-2F_2\text{cos}\alpha =0.}\end{array}$ (4') Számítsuk ki $F$-et $\text{sin}\alpha \ne 0$ esetén! Ekkor $\begin{array}{c}{\displaystyle F=ml{\omega }^2\text{cos}\alpha -\left(m+M\right)g\mathrm{.}}\end{array}$ (6) A rendszer külső erőhatás nélkül is nyugalomban van, ha $F=0$. Ez akkor teljesül, ha $\alpha$ az (5)  egyenletnek megfelelő ${\alpha }_0$ értéket veszi fel. Ha a $\alpha >{\alpha }_0$, akkor $F<0$, tehát a $M$ tömegű testet elengedve az lefelé mozdul. Ha $\alpha <{\alpha }_0$, akkor $F>0$, $M$-et elengedve az felfelé mozdul. Az (5)  egyenlettel jellemzett egyensúlyi helyzet tehát mindig stabil. Az $\alpha =0$, $\overline{AM}=2l$ egyensúlyi helyzet stabilitása $\omega$ értékétől függ. Ha $\omega <{\omega }_{\underset{}{\overset{}{\text{min}}}}$, akkor $\left(m+M\right)g>ml{\omega }^2\text{cos}\alpha$, $F<0$ bármely $\alpha$-ra. Az $M$ tömeg tehát csak felfelé ható erővel tartható egyensúlyban, elengedve visszatér az $\alpha =0$  helyzetbe. Ekkor az egyensúlyi helyzet stabil. Ha $\omega >{\omega }_{\underset{}{\overset{}{\text{min}}}}$, $0<\alpha <{\alpha }_0$ esetén $F>0$. Így elengedve, a rendszer az $\alpha ={\alpha }_0$ helyzet felé mozdul, az $\alpha =0$ egyensúlyi helyzet labilis. A 2. ábrán a stabil egyensúlyi helyzetet folytonos, a labilis egyensúlyi helyzetet szaggatott vonallal jelöltük.