Feladat:	1500. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bene Gyula ,  Csordás András ,  Czuczor Lajos ,  Frey István ,  Kaufmann Zoltán ,  Kilián Imre ,  Mechler Ferenc ,  Pakai Tibor ,  Samu Péter ,  Sas Viktor
Füzet:	1978/november, 182 - 184. oldal		PDF  |  MathML
Témakör(ök):	Kötélsúrlódás, Rögzített tengely körüli forgás (Merev testek mozgásegyenletei), Határozott integrál, Feladat
Hivatkozás(ok):	Feladatok: 1978/április: 1500. fizika feladat

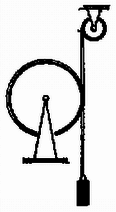
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Használjuk az $1447.$ feladat megoldásának jelöléseit (l. az $1.$ ábrát)! Az egyes testek mozgásegyenlete ugyanaz, mint az $1447.$ feladatban: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle ma=mg-K_2\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle \left[\left(1/2\right)m_1{r}_1^2\right]{\beta }_1=K_1{r}_1\mathrm{,}\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle \left[\left(1/2\right)m_2{r}_2^2\right]{\beta }_2=S{r}_2=\left(K_2-K_1\right)r_2\mathrm{,}}\hfill & \text{(<mn>3</mn>)}\end{array}}$ és továbbra is fennáll az $a$ és a ${\beta }_1$ közötti, a kötél nyújthatatlanságából eredő összefüggés: 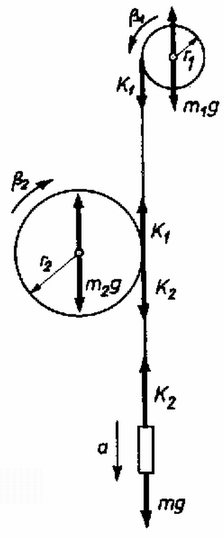$\begin{array}{c}{\displaystyle a=r_1{\beta }_1\mathrm{.}}\end{array}$ (4)     1. ábra   A súrlódási együttható értékétől függően két eset lehetséges: a kötél vagy tapad a nagy hengerhez, vagy csúszik rajta. Vizsgáljuk az utóbbi esetet! Ekkor $\begin{array}{c}{\displaystyle a\ge r_2{\beta }_2\mathrm{,}}\end{array}$ (5) tehát még egy egyenletre van szükségünk. Tekintsük a kötélnek egy kis $\text{d<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>φ</mi></math>}$ középponti szöghöz tartozó darabját ($2.$ ábra)! A kötéldarab végeinél ható erők nagyságát jelöljük $K\left(\phi \right)$, ill. $K\left(\phi +\text{d<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>φ</mi></math>}\right)$-vel! Az ábráról leolvasható, hogy a kötéldarab $\begin{array}{c}{\displaystyle \text{d}N\cong K\left(\phi \right)\text{d}\phi }\end{array}$ (6) nagyságú erővel nyomja a hengert. Mivel a kötél csúszik, 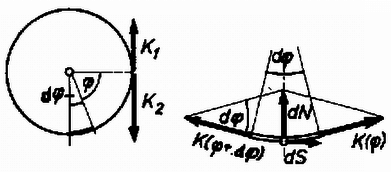$\begin{array}{c}{\displaystyle \text{d}S=\mu \text{d}N\mathrm{.}}\end{array}$ (7)     2. ábra   A súlytalan kötéldarabra ható erőknek ki kell egyensúlyozniuk egymást, különben a gyorsulás végtelenül nagy lenne, ezért $\begin{array}{c}{\displaystyle K\left(\phi +\text{d}\phi \right)-K\left(\phi \right)=\text{d}s\mathrm{,}}\end{array}$ (8) azaz $\begin{array}{c}{\displaystyle K\left(\phi +\text{d}\phi \right)-K\left(\phi \right)=\mu K\left(\phi \right)\text{d}\phi \mathrm{.}}\end{array}$ (9) A $\left(6\right)$, $\left(8\right)$ és $\left(9\right)$ összefüggések közelítőek, annál pontosabbak, minél kisebb a $\text{d}\phi$. A $\text{d}\phi \to 0$ határátmenettel $\left(9\right)$-ből a $\begin{array}{c}{\displaystyle \frac{\text{d}K\left(\phi \right)}{\text{d}\phi }=\mu K\left(\phi \right)}\end{array}$ (10) differenciálegyenletet kapjuk. Rendezzük át az egyenletet, és integráljuk mindkét oldalt ${\phi }_1\mathrm{,}{\phi }_2$ határok között: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \underset{{\phi }_1}{\overset{{\phi }_2}{\int }}\frac{\text{d}K\left(\phi \right)}{K\left(\phi \right)}=\mu \underset{{\phi }_1}{\overset{{\phi }_2}{\int }}\text{d}\phi ;}\hfill & \text{(<mn>11</mn>)}\\ \hfill {\displaystyle \text{ln}\frac{K\left({\phi }_2\right)}{K\left({\phi }_1\right)}=\mu \left({\phi }_2-{\phi }_1\right)\mathrm{.}}\hfill \\ \hfill {\displaystyle K\left({\phi }_2\right)=K\left({\phi }_1\right)\cdot e^{\mu \left({\phi }_2-{\phi }_1\right)}\mathrm{.}}\hfill & \text{(<mn>12</mn>)}\end{array}}$ Felhasználva, hogy $K\left(0\right)=K_1$; $K\left(2\pi \right)=K_2$, $\left(12\right)$-ből ${\phi }_1=0$, ${\phi }_2=2\pi$ helyettesítéssel nyerjük: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle K\left(\phi \right)}& {\displaystyle =K_1\cdot e^{\mu \phi }\mathrm{,}}\hfill & \text{(<mn>13</mn><mi>a</mi>)}\\ \hfill {\displaystyle K_2}& {\displaystyle =K_1\cdot e^{2\pi \mu }\mathrm{.}}\hfill & \text{(<mn>13</mn><mi>b</mi>)}\end{array}}$ Ezzel megkaptuk $\left(10\right)$-nek azt a megoldását, amely kielégíti a $K\left(0\right)=K_1$ kezdeti feltételt (vö. a januári számban kitűzött $1479.$ feladattal). Az $\left(1\right)-\left(4\right)$ egyenletrendszert a $\left(13b\right)$ egyenlet teszi teljessé. A megoldás: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a}& {\displaystyle =g\cdot \frac{2m}{2m+m_{1}c};}\hfill \\ \hfill {\displaystyle {\beta }_1}& {\displaystyle =\frac{g}{r_1}\cdot \frac{2m}{2m+m_{1}c};}\hfill \\ \hfill {\displaystyle K_1}& {\displaystyle =mg\cdot \frac{m_1}{2m+m_{1}c};}\hfill & \text{(<mn>14</mn>)}\\ \hfill {\displaystyle K_2}& {\displaystyle =mg\cdot \frac{m_1}{2m+m_{1}c}\cdot c;}\hfill \\ \hfill {\displaystyle {\beta }_2}& {\displaystyle =\frac{g}{r_2}\cdot \frac{2m}{2m+m_{1}c}\cdot \frac{m_1}{m_2}\left(c-1\right);c=e^{2\pi \mu }\mathrm{.}}\hfill \end{array}}$ Ez a megoldás akkor helyes, azaz a kötél akkor csúszik valóban a hengeren, ha $\left(5\right)$ teljesül. Ez a feltétel $\left(14\right)$ behelyettesítésével a ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{m_1}{m_2}\left(c-1\right)\le \mathrm{1,}}\hfill & \text{(<mn>15</mn>)}\\ \hfill {\displaystyle \mu \le \frac{1}{2\pi }\cdot \text{ln}\frac{m_1+m_2}{m_1}}\hfill \end{array}}$ alakra hozható. Ha $\mu$ a jobb oldalon álló értéknél nagyobb, a kötél nem tud megcsúszni a hengeren. Ebben az esetben $\left(10\right)$ és $\left(13b\right)$ nem igaz, de $\left(5\right)$-ben az egyenlőség teljesül, és ez adja az ötödik egyenletet. A keresett mennyiségek ebben az esetben ${\displaystyle \begin{array}{c}\hfill {\displaystyle a=g\frac{2m}{2m+m_1+m_2};{\beta }_1=\frac{g}{r_1}\frac{2m}{2m+m_1+m_2};}\hfill \\ \hfill {\displaystyle {\beta }_2=\frac{g}{r_2}\cdot \frac{2m}{2m+m_1+m_2};K_1=m_{1}g\frac{m}{2m+m_1+m_2};}\hfill \end{array}}$ $\begin{array}{c}{\displaystyle K_2=mg\cdot \frac{m_1+m_2}{2m+m_1+m_2}\mathrm{.}}\end{array}$    Czuczor Lajos (Budapest, Fazekas M. Gyak. Gimn., III. o. t.) és  Bene Gyula (Miskolc, Földes F. Gimn., III. o. t.)  dolgozata alapján   II. megoldás. A $K_1$ és a $K_2$ közötti összefüggés a következő úton is megkapható: a kötélnek a hengerre tekeredő részét $n$ egyenlő részre osztva, az $i$-edik darabra $\left(9\right)$ alapján $\begin{array}{c}{\displaystyle K\left(i\frac{2\pi }{n}\right)-K\left[\left(i-1\right)\frac{2\pi }{n}\right]=\mu \frac{2\pi }{n}\cdot K\left[\left(i-1\right)\frac{2\pi }{N}\right]\mathrm{,}}\end{array}$ (16) azaz $\begin{array}{c}{\displaystyle K\left(i\frac{2\pi }{n}\right)=\left(1+\frac{\mu 2\pi }{n}\right)K\left[\left(i-1\right)\frac{2\pi }{n}\right]={\left(1+\frac{\mu 2\pi }{n}\right)}^{i}K\left(0\right)\mathrm{,}}\end{array}$ (17) ahonnan $\begin{array}{c}{\displaystyle K_2=K_1{\left(1+\frac{\mu 2\pi }{n}\right)}^n\mathrm{.}}\end{array}$ (18) Ez az egyenlőség annál pontosabb, minél nagyobb $n$. A felosztást finomítva megkapjuk $\left(13b\right)$-t: $\begin{array}{c}{\displaystyle K_2=K_1\cdot \underset{n\to \infty }{\overset{}{\text{lim}}}{\left(1+\frac{2\pi \mu }{n}\right)}^n=K_1\cdot e^{2\pi \mu }\mathrm{.}}\end{array}$ (19)    Kilián Imre (Debrecen, KLTE Gyak. Gimn., IV. o. t.)