Kezdőlap


Feladat:	1497. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Benkő Zsigmond , Csordás András , Kovács Zoltán , Szabó Edit
Füzet:	1978/december, 233 - 235. oldal		PDF \| MathML
Témakör(ök):	Arkhimédész törvénye, Erők forgatónyomatéka, Erőrendszer eredője, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1978/április: 1497. fizika feladat

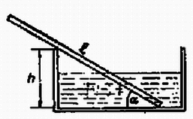
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A pálcára az ábrán látható erők hatnak. A megmozdulás pillanatáig a pálcára ható erők vízszintes, ill. függőleges összetevőinek eredője nulla:

\begin{matrix} S_{2} cos α + S_{1} - N_{2} sin α = 0, \end{matrix}

(1)

\begin{matrix} G - F - N_{1} - N_{2} cos α - S_{2} sin α = 0. \end{matrix}

(2)

Az erők forgatónyomatékára vonatkozó egyenlet a pálca két végpontjára:

\begin{matrix} G [h ctg α - (l / 2) cos α] - F [h ctg α - (x / 2) ctg α] - N_{1} h ctg α + S_{1} h = 0, \end{matrix}

(3)

\begin{matrix} G (l / 2) cos α - F (x / 2) ctg α - N_{2} h / sin α = 0. \end{matrix}

'

)

A pálca súlya

G = l A ϱ_{pálca} g

, a felhajtóerő

F = (x / sin α) A ϱ_{víz} g

(

A

a pálca keresztmetszetének területe).

A

-t kiküszöbölve

\begin{matrix} F = \frac{x}{l sin α} r G, \end{matrix}

(4)

ahol

\begin{matrix} r = \frac{ϱ_{viz}}{ϱ_{pálca}} . \end{matrix}

A pálca kétféleképpen mozdulhat meg: 1. a pálca az edény aljára támaszkodó vége felemelkedik, 2. a pálca megcsúszik. Foglalkozzunk először az első esettel.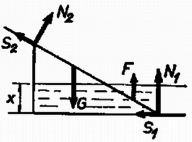

1. A felemelkedés pillanatában

N_{1} = 0

és

S_{1} = 0

S_{2} ≦ μ N_{2}

. Az utóbbi feltétel alapján (1)-ből

\begin{matrix} S_{2} = N_{2} tg α ≦ μ N_{2} . \end{matrix}

Ezért az 1. eset megvalósulásához szükséges feltétel:

\begin{matrix} μ ≧ tg α . \end{matrix}

(5)

A pálca megmozdulásához szükséges vízmagasságot az (1)‐(4) egyenletrendszer megoldásával határozhatjuk meg

N_{1} = S_{1} = 0

behelyettesítésével. Másodfokú egyenletre jutunk, amelynek gyökei

\begin{matrix} x_{1,2} = h \pm \sqrt[]{h^{2} - (l / r) (2 h - l sin α) sin α .} \end{matrix}

A két gyök közül az

\begin{matrix} x_{1} = h - \sqrt[]{h^{2} - (l / r) (2 h - l sin α) sin α} \end{matrix}

(6)

a fizikailag érdekes, mivel

x_{1} < x < h

esetén

x

-et növelve

F

gyorsabban nő, mint ahogy az edény peremére vonatkozó karja csökken, tehát bármely

x_{1}

és

h

közé eső vízmagasságra felemelkedik a pálca.
Ha a diszkrimináns negatív, a pálca egyáltalán nem mozdul meg. Ez akkor áll fenn, ha

\begin{matrix} ϱ_{pálca} > ϱ_{víz} \frac{h^{2}}{l (2 h - l sin α) sin α} . \end{matrix}

(7)

μ < tg α

esetén az I. eset nem valósulhat meg, ekkor a pálca lecsúszhat. A határesetben

S_{1} = μ N_{1}

és

S_{2} = μ N_{2},

ezeket behelyettesítve az (1)‐(4) egyenletrendszerbe, a megmozduláshoz szükséges vízmagasság meghatározható.

[

Célszerű most a

(3')

forgatónyomaték egyenletet használni.

]

x

-re most is másodfokú egyenlet adódik, amelynek két gyöke közé eső vízmagasság esetén mozdulhat meg a pálca. Ez azt jelenti, hogy a kisebb gyök a fizikailag érdekes, mégpedig

\begin{matrix} x_{1} = \frac{h}{[μ + (1 / μ)] sin α cos α} - \\ - \sqrt[]{{[\frac{h}{[μ + (1 / μ)] sin α cos α}]}^{2} - \frac{2 h l}{[μ + (1 / μ)] r cos α} + \frac{l^{2} {sin}^{2} α}{r}} . & (8) \end{matrix}

Megcsúszásról csak akkor beszélhetünk, ha

N_{1} \geq 0

és

N_{2} \geq 0

. Az egyenletrendszerből

\begin{matrix} N_{2} = \frac{G - F}{[μ + (1 / μ)] sin α}, \\ N_{1} = N_{2} [(1 / μ) sin α - cos α] . \end{matrix}

μ = tg α

esetén

(1 / μ) sin α - cos α > 0

, így

N_{1}

és

N_{2}

akkor lesz nemnegatív, ha

G \geq F

, ahonnan

(4)

felhasználásával a megcsúszás szükséges feltétele;

\begin{matrix} x \leq \frac{l sin α}{r} . \end{matrix}

Ezek alapján nem nehéz belátni, hogy a megcsúszás pontosan akkor következik be, ha a

(8)

alatti

x_{1}

értékre az

\begin{matrix} x_{1} < \frac{l sin α}{r} \end{matrix}

(9)

feltétel teljesül, éspedig a pálca az

x_{1}

vízmagasság túllépése után csúszik meg.
A pálca víz beeresztése nélkül is lecsúszik, ha

x_{1} < 0

. Ez akkor teljesül, ha

(8)

-ban a négyzetgyök alatti utolsó két tag összege pozitív. Innen a ‐ közvetlenül is belátható

\begin{matrix} μ + \frac{1}{μ} > \frac{h}{sin α} \frac{4}{l sin 2 α} \end{matrix}

(10)

egyenlőtlenség adódik,

μ

-re felső korlátot ad.
Nem csúszik le a pálca, ha

x_{1} > h

, vagy ha

(8)

-ban a négyzetgyök alatti kifejezés negatív.
Vizsgáljuk meg, mi történik a feladatban megadott számpéldák esetén. (Sajnálatos elírás következtében a feladat szövege

l = 20

cm-es adattal jelent meg, ilyen adattal az ábra szerinti elrendezés nem valósulhat meg. Használjuk most az

l = 30

cm-es adatot.)

tg α = 1 / \sqrt[]{3} \approx 0, 58

, így

μ = 0, 6

esetén a pálca felemelkedik.

μ = 0, 4

és

0, 2

esetén lecsúszik.
a)

μ = 0, 6

súrlódási együttható esetén a pálca felemelkedik. A megmozduláshoz szükséges vízmagasság

(6)

-ból

\begin{matrix} x_{1} \approx 4, 1 cm . \end{matrix}

Nem emelkedne fel a pálca, ha sűrűsége túl nagy lenne.

(7)

alapján ennek feltétele

\begin{matrix} ϱ_{pálca} > 1, 07 ϱ_{víz} . \end{matrix}

A pálca víz nélkül is lecsúszik, ha

(10)

-ből

\begin{matrix} μ + (1 / μ) > 3, 7, \end{matrix}

ahonnan a fizikailag reális tartomány

\begin{matrix} μ < 0, 29. \end{matrix}

A c) esetben

(μ = 0, 2)

tehát a pálca a víz beengedése előtt sem marad nyugalomban.
A b) esetben

(μ = 0, 4)

(8)

alapján a pálca akkor csúszik meg, ha a víz mélysége nagyobb, mint

\begin{matrix} x_{1} = 1, 4 cm, \end{matrix}

erre ui. teljesül a

(9)

feltétel:

\begin{matrix} x_{1} < 9 cm . \end{matrix}

Megjegyzés. A hibás számadat következtében többen más adatokat használtak, illetve csak algebrailag számoltak. Ezeket a dolgozatokat helyesnek fogadtuk el. Mások az ábra elrendezését változtatták meg úgy, hogy a pálca nem az oldalfal tetejére, hanem belső oldalára támaszkodott. Mivel ekkor az eredmény taglalása lényegesen egyszerűbb, az ilyen ‐ egyébként hibátlan ‐ dolgozatok

3

pontot kaptak.