Kezdőlap


Feladat:	1495. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Györgyi Géza
Füzet:	1979/január, 35 - 37. oldal		PDF \| MathML
Témakör(ök):	Doppler-hatás (Doppler-effektus), Feladat
Hivatkozás(ok):	Feladatok: 1978/április: 1495. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jellemezzük a $v$ sebességű autó helyzetét az $r$ sugarú körpályán a $φ$ középponti szöggel! Ha az autó a megfigyelő mellett van, akkor $φ = 0$ , s ezután a $φ$ szög nő.

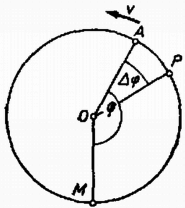1. ábra

Először kiszámítjuk, a pálya mely

P

pontjáról indult ki az a hanghullám, amelyet a megfigyelő (

M

) akkor hall, amikor az autó (

A

) a

φ

-vel jelölt helyzetben van (1. ábra). A versenyautó a

\hat{P A}

ívet ugyanannyi idő alatt tette meg, amennyi időre a hangnak volt szüksége ahhoz, hogy

P

-ből a megfigyelőhöz eljusson. Ezért

\begin{matrix} \frac{\hat{P A}}{v} = \frac{\bar{P M}}{c}, \end{matrix}

ahol

c

a hangsebesség. Vagyis a

\bar{P M} / 2 = r sin [(φ - Δ φ) / 2]

összefüggést felhasználva:

\begin{matrix} \frac{r Δ φ}{v} = \frac{2 r sin [(φ - Δ φ) / 2]}{c} = (2 r / c) [sin (φ / 2) cos (Δ φ / 2) - sin (Δ φ / 2) cos (φ / 2)] . \end{matrix}

(1)

v

elegendően kicsiny

c

-hez képest, akkor

Δ φ

is kicsi, és alkalmazhatjuk a

\begin{matrix} sin (Δ φ / 2) \approx Δ φ / 2 és a cos (Δ φ / 2) \approx 1 \end{matrix}

(2a‐b)

közelítő formulákat. Ezek alapján az (1) egyenletet átalakíthatjuk, és

Δ φ

-re a

\begin{matrix} Δ φ = \frac{2 sin (φ / 2)}{(c / v) + cos (φ / 2)} \end{matrix}

(3)

kifejezést kapjuk. Könnyen belátható, hogy képletünk a teljes (

0,2 π

) intervallumban érvényes.
Jelöljük a

P

pont helyzetét

φ - Δ φ = ψ

-veI! Az autó itt

f

frekvenciájú hangot bocsátott ki, amelyet a megfigyelő más (

f'

) frekvenciájúnak hall, mert az autó a megfigyelőhöz viszonyítva mozgott. Ez az úgynevezett Doppler-hatás.

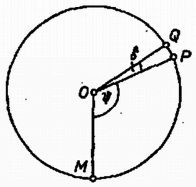2. ábra

Számítsuk ki a megfigyelő által észlelt hang rezgésszámát (2. ábra)! A hangforrás a

\hat{P Q}

ív megtétele alatt sugározzon ki egy periódusnyi hanghullámot! Ekkor a

\hat{P Q}

ívet épp a periódusidő alatt teszi meg:

\begin{matrix} \hat{P Q} = v T . \end{matrix}

Mivel

T = 1 / f

és

\hat{P Q} = r δ

δ

-ra a

\begin{matrix} δ = v / (r f) \end{matrix}

(4)

kifejezést kapjuk. A periódus kezdetét a megfigyelő a jel kibocsátását követő

\begin{matrix} t_{1} = \bar{P M} / c = (2 r / c) sin (ψ / 2) \end{matrix}

idő múlva hallja. A periódust záró jelet a forrás a periódusidővel később sugározza ki, ezért az

\begin{matrix} t_{2} = T + \bar{Q M} / c \end{matrix}

(5)

idő múlva érkezik a megfigyelőhöz. A

\bar{Q M} = 2 r sin [(ψ + δ) / 2]

kifejezést felhasználva, átalakítás után a

\begin{matrix} t_{2} = (1 / f) + (2 r / c) [sin (ψ / 2) cos (δ / 2) + cos (ψ / 2) sin (δ / 2)] \end{matrix}

(6)

formulát kapjuk. Mivel a gyakorlatban előforduló adatok mellett

δ

értéke elég kicsiny ahhoz, hogy szögfüggvényeire a (2) közelítő képleteket alkalmazhassuk, (6) így módosul:

\begin{matrix} t_{2} = (1 / f) + (2 r / c) sin (ψ / 2) + [v / (f c)] cos (ψ / 2) . \end{matrix}

A periódus kezdeti és végső jelének az

M

pontba való beérkezése közötti időkülönbség az észlelt periódusidő:

\begin{matrix} T' = 1 / f' = t_{2} - t_{1} = (1 / f) + [v / (f c)] cos (ψ / 2), \end{matrix}

azaz

\begin{matrix} f' = \frac{f}{1 + (v / c) cos (ψ / 2)} . \end{matrix}

(7)

Ez a formula a teljes (

0,2 π

) tartományon érvényes.
A

ψ = φ - Δ φ

képlet alapján

\begin{matrix} f' = \frac{1}{1 + (v / c) cos [(φ - Δ φ) / 2]} . \end{matrix}

A nevezőt átalakítva a (2) közelítő formulák és a (3) képlet felhasználásával az észlelt frekvenciát az

\begin{matrix} f' = \frac{f}{1 + \frac{v}{c} [cos \frac{φ}{2} + \frac{sin^{2} (φ / 2)}{(c / v) + cos (φ / 2)}]} = \frac{f}{1 + \frac{cos (φ / 2) + v / c}{cos (φ / 2) + c / v}} \end{matrix}

(8)

összefüggéssel írhatjuk le. Ha

v ≪ c

, akkor az

\begin{matrix} f' = \frac{f}{1 + (v / c) cos (φ / 2)} \end{matrix}

(9)

formulát kapjuk.

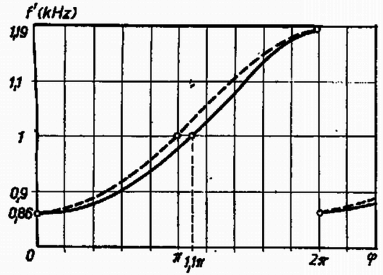3. ábra

Györgyi Géza

Megjegyzések. 1. Ábrázoljuk a kapott függvényeket (3. ábra)! Legyen

f = 1 kHz

v = 200

km/óra. Szaggatott vonallal jelöltük a

Δ φ

-vel nem korrigált (9) függvényt, folytonossal a (8) képletben szereplő függvény görbéjét. Az ábráról leolvasható, hogy a

0 < φ < π

, ill. a

0 < φ < 1

1 π

intervallumban a hang mélyebb, a

π < φ < 2 π

, ill. az 1,

1 π < φ < 2 π

tartományban magasabb annál, amit az autóval együtt mozgó megfigyelő hallana. Amikor az autó a megfigyelőnél halad el, a függvény szerint a hangmagasság ugrásszerűen megváltozik. Ez annak a következménye, hogy ebben a pontban a megfigyelő és az autó távolságát zérusnak tekintettük. A valóságban a hangmagasság véges idő alatt csökken le.
2. Vizsgáljuk meg, mekkora hibát jelent a (2) közelítő képletek alkalmazása! Ha

(Δ φ) < 0,245

, akkor a (2) formulák hibája kisebb

1 %

-nál (l. Négyjegyű függvénytáblázatok; Matematikai, fizikai, kémiai összefüggések, 84. old.).

Δ φ

értéke nyilván akkor a legnagyobb, amikor a hang útja a leghosszabb, azaz

2 r

. A

P

pont ekkor az

M

-mel azonos átlón, vele átellenesen helyezkedik el, és

Δ φ_{max}

-ra az

r Δ φ_{max} / v = 2 r / c

egyenletet kapjuk. Innen

Δ φ_{max} = 2 v / c

. A hangsebességet

340 m/s

-nak tekintve az

1 %

-os hiba feltétele:

v < 300 km/ó

. Különböző hibaszámítási módszerek felhasználásával ‐ amelyek közül a leglényegesebb az az eljárás, amellyel egy függvény hibáját számolhatjuk ki az argumentum hibájának ismeretében ‐ a (8) kifejezés hibája is kiszámítható.
A (2) képleteknek a delta szögfüggvényeire való alkalmazása (6) esetében viszont nem vezet pontatlansághoz.

δ

értékét ugyanis bármilyen kicsire választhatjuk, ha egy periódus helyett annak tetszőleges, de rögzített törtrészével végezzük el számításainkat.
3. Vegyük észre, hogy az észlelt frekvencia kiszámításakor nem használtuk ki, hogy az autó pályája kör. Bármilyen más módon mozgó hangforrás egy elegendően kicsiny pályarészletének kezdő- és végpontján, valamint a megfigyelő helyén keresztül rajzolható egy kör. Ha

ψ

-vel az előzőekhez hasonlóan a megfigyelő és a hangkibocsájtás helyének középponti szögét jelöljük, akkor a (7) formulához jutunk. A

ψ / 2

szög a mozgó forrás sebességvektora és az őt a megfigyelővel összekötő szakasz által bezárt szöggel egyezik meg. Ebből látszik, hogy a Doppler-hatásnál csak a távolodás vagy közeledés sebessége lényeges. A megoldók többsége azt, hogy az észlelt frekvencia egyenletében a sebességnek csak ez a komponense szerepel, minden számítás nélkül természetesnek tekintette, erre maximális pontszámot nem adhattunk.