Kezdőlap


Feladat:	1482. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Madi Tibor , Szabó László
Füzet:	1978/november, 172 - 175. oldal		PDF \| MathML
Témakör(ök):	Pontrendszerek mozgásegyenletei, Nyomóerő, kötélerő, Tapadó súrlódás, Csúszó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1978/február: 1482. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az első pillanatban az alsó deszka sebessége $v_{0}$ , a felsőé nulla. Érintkező felületeik elmozdulnak egymáson, csúszó súrlódási erők lépnek fel. Tegyük fel, hogy a mozgás során a felső deszka nem billen le az alsóról! Ebben az esetben addig csúsznak egymáson, amíg sebességük egyenlővé nem válik. Ha a felső deszkára ható tapadási súrlódási erő nem elegendően nagy ahhoz, hogy ezután együtt mozogjanak, akkor a felső deszka a mozgás irányában csúszik az alsóhoz képest mindaddig, amíg mindkét deszka meg nem áll.
A felső test akkor nem billen le, ha a mozgás első szakaszában a $Δ s_{1}$ relatív elmozdulás nem nagyobb $l / 2$ -nél, és a közös sebesség elérésétől a megállásig az előzővel ellentétes irányú $Δ s_{2}$ relatív elmozdulás nem nagyobb $Δ s_{1} + (l / 2)$ -nél.

1. ábra

Tekintsük a mozgás első szakaszát! A deszkák függőleges irányú gyorsulása nulla. A felső testre ezért felírhatjuk az

1. ábra

alapján az

\begin{matrix} m_{1} g - N_{1} = 0 \end{matrix}

egyenletet, az alsó deszkára pedig az

\begin{matrix} m_{2} g + N_{1} - N_{2} = 0 \end{matrix}

összefüggés teljesül, ahol

N_{1}

a két deszka közötti,

N_{2}

a talaj és az alsó test közötti nyomóerő. Az egyenleteket megoldva az

\begin{matrix} N_{1} & = m_{1} g, \\ N_{2} & = (m_{1} + m_{2}) g \end{matrix}

eredményhez jutunk.
A deszkák vízszintes irányú gyorsulásait a mozgásegyenletekből számíthatjuk ki:

\begin{matrix} m_{1} a_{1} & = S, & (1) \\ m_{2} a_{2} & = - S - F . & (2) \end{matrix}

A csúszási súrlódási erőkre az

\begin{matrix} S & = μ_{1} | N_{1} | = μ_{1} m_{1} g, \\ F & = μ_{2} | N_{2} | = μ_{2} (m_{1} + m_{2}) g \end{matrix}

egyenletek állnak fenn. Ezeket

(1)

-be és

(2)

-be helyettesítve a gyorsulásokat kifejezhetjük:

\begin{matrix} a_{1} = μ_{1} g, & (3) \\ a_{2} = - g (μ_{2} \frac{m_{1} + m_{2}}{m_{2}} + μ_{1} \frac{m_{1}}{m_{2}}) . & (4) \end{matrix}

A mozgás megindulásától számított

t'

idő múlva a két test sebessége azonos lesz:

\begin{matrix} v_{0} + a_{2} t' = v_{1} = a_{1} t', \end{matrix}

innen

\begin{matrix} t' = \frac{v_{0}}{a_{1} - a_{2}} . \end{matrix}

(5)

Mivel a deszkák azonos irányban mozognak, a relatív elmozdulás a két deszka által megtett utak különbsége:

\begin{matrix} Δ s_{1} = s_{2} - s_{1} = v_{0} t' + (1 / 2) a_{2} t'^{2} - (1 / 2) a_{1} t'^{2} . \end{matrix}

(5)

felhasználásával a

\begin{matrix} Δ s_{1} = \frac{1}{2} \frac{v_{0}^{2}}{a_{1} - a_{2}} \end{matrix}

kifejezést kapjuk.

(3)

és

(4)

alapján a

\begin{matrix} Δ s_{1} \leq l / 2 \end{matrix}

feltétel a

\begin{matrix} \frac{v_{0}^{2} m_{2}}{2 g (μ_{1} + μ_{2}) (m_{1} + m_{2})} \leq \frac{l}{2} \end{matrix}

alakot ölti. Ez

v_{0}

-ra a

\begin{matrix} v_{0} \leq \sqrt[]{\frac{l g}{m_{2}} (μ_{1} + μ_{2}) (m_{1} + m_{2})} \end{matrix}

(6)

megszorítást jelenti.
A mozgás további vizsgálatánál feltesszük, hogy a csúszási és a tapadási súrlódási együttható megegyezik.

2. ábra

Ha a deszkák többé nem csúsznak egymáson, akkor gyorsulásuk megegyezik. Írjuk fel a mozgásegyenleteket (

2. ábra

\begin{matrix} m_{1} a & = S; \\ m_{2} a & = - F - S; \end{matrix}

ahol

S

tapadási;

F

csúszási súrlódási erő:

\begin{matrix} | S | & \leq μ_{1} | N_{1} | = μ_{1} m_{1} g, & (7) \\ F & = μ_{2} | N_{2} | = μ_{2} (m_{1} + m_{2}) g . \end{matrix}

A mozgásegyenletekből

S

-et kifejezzük:

\begin{matrix} S = μ_{2} m_{1} g . \end{matrix}

(7)

egyenlőtlenségbe

S

értékét behelyettesítjük, és egyszerűsítés után az együtt mozgás következő feltételéhez jutunk:

\begin{matrix} μ_{2} \leq μ_{1} . \end{matrix}

(8)

Ha ez teljesül, a felső deszka nem eshet le az alsóról, azaz ekkor a

(6)

feltétel elegendő.
Ha

(8)

nem áll fenn, akkor a felső test előre csúszik az alsóhoz képest, ezért a megállásig nagyobb utat tesz meg, mint az alsó test. A felső deszkát a csúszás miatt ugyanakkora abszolút értékű erő lassítja, mint amekkora eddig gyorsította, tehát a felső test a mozgás megkezdésétől számított

2 t'

idő elteltével áll meg. Ezek alapján elkészíthetjük a deszkák sebesség-idő diagramját (

3. ábra

; szaggatott vonallal az alsó deszka

v (t)

függvényét jelöltük).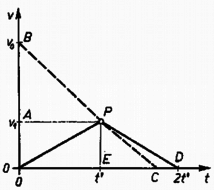

3. ábra

Az ábra alapján a területekre fennáll:

\begin{matrix} T (O P B_{▵}) > T (O P A_{▵}) = T (O E P_{▵}) = T (E D P_{▵}) - T (C D P_{▵}) . \end{matrix}

Vegyük észre, hogy

v_{1}

eléréséig a relatív elmozdulás

\begin{matrix} Δ s_{1} = T (O P B_{▵}), \end{matrix}

s ettől az időponttól az

m_{1}

tömegű deszka megállásáig az egymáshoz viszonyított ellenkező irányú elmozdulás

\begin{matrix} Δ s_{2} = T (C D P_{▵}) . \end{matrix}

Következésképpen

\begin{matrix} Δ s_{1} > Δ s_{2}; \end{matrix}

\begin{matrix} Δ s_{1} + l / 2 \geq Δ s_{2} \end{matrix}

feltétel így automatikusan teljesül. Ezért a felső test előre nem billenhet le.
Láttuk, ha a

(6)

feltétel teljesül, bármilyen legyen is a mozgás a közös sebesség elérése után, a felső deszka már nem billenhet le. A

(6)

egyenlőtlenség tehát szükséges és egyben elegendő feltétele annak, hogy a felső test ne essék le az alsóról.

Szabó László (Csongrád, Batsányi J. Gimn., II. o. t.)