Feladat:	1471. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bene Gyula ,  Benkő Zsigmond ,  Csikós Balázs ,  Csók Tibor ,  Csordás András ,  Frey István ,  Hlavathy Zoltán ,  Kaufmann Zoltán ,  Mechler Ferenc ,  Németh Gábor ,  Németh Róbert ,  Sas Viktor ,  Simon István ,  Vesztergombi Antal
Füzet:	1978/május, 233 - 236. oldal		PDF  |  MathML
Témakör(ök):	Gördülés vízszintes felületen, Tapadó súrlódás, Csúszó súrlódás, Függvények grafikus elemzése, Feladat
Hivatkozás(ok):	Feladatok: 1977/december: 1471. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.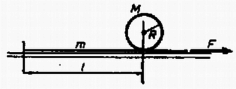 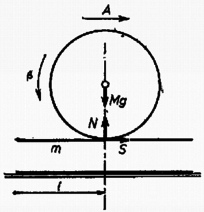    A golyóra a következő erők hatnak (1. ábra): súlyerő ($Mg$), nyomóerő ($N$), súrlódási erő ($S$). A fóliára ható erők (2. ábra): súlyerő ($mg$), húzóerő ($F$), nyomóerők ($N$ és $N_1$), súrlódási erők ($S$ és $S_1$). A gyorsulások és a szöggyorsulás jelölését, valamint a pozitív irányokat is feltüntettük az ábrán.     1. ábra 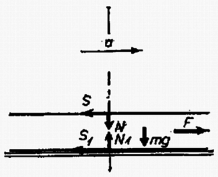    2. ábra A mozgásegyenletek: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle MA}& {\displaystyle =S\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle 0}& {\displaystyle =Mg-N\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle \Theta \beta }& {\displaystyle =SR\mathrm{,}}\hfill & \text{(<mn>3</mn>)}\\ \hfill {\displaystyle ma}& {\displaystyle =F-S-S_1\mathrm{,}}\hfill & \text{(<mn>4</mn>)}\\ \hfill {\displaystyle 0}& {\displaystyle =mg+N-N_1\mathrm{.}}\hfill & \text{(<mn>5</mn>)}\end{array}}$ Itt $\begin{array}{c}{\displaystyle \Theta =\left(2/5\right)M{R}^2}\end{array}$ (6) a golyó tehetetlenségi nyomatéka. $F$ nagyságától függően három esetet különböztetünk meg: a) $F$ elég kicsi. Ekkor a fólia odatapad az asztalhoz, a golyó sem mozog: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a=0;}\hfill & \text{(<mn>7</mn>)}\\ \hfill {\displaystyle A=0.}\hfill & \text{(<mn>8</mn>)}\end{array}}$ Az (1)‐(8) egyenletrendszerből kapjuk, hogy $\begin{array}{c}{\displaystyle \beta =\mathrm{0,}S=\mathrm{0,}{S}_1=F;}\end{array}$ és természetesen a golyó szögsebessége is nulla: $\begin{array}{c}{\displaystyle \omega =0.}\end{array}$ Az a) eset megvalósulásának feltétele, hogy $\begin{array}{c}{\displaystyle S_1\le \mu N_1\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle F\leqq \mu \left(m+M\right)g}\end{array}$ (9) legyen.   b) Ha $\begin{array}{c}{\displaystyle F>\mu \left(m+M\right)g\mathrm{,}}\end{array}$ de nem olyan nagy, hogy a golyó megcsússzék a fólián, akkor a fólia és a talaj közötti súrlódásra az $\begin{array}{c}{\displaystyle S_1=\mu N_1\mathrm{,}}\end{array}$ (10) valamint a golyó csúszásmentes gördülésére az $\begin{array}{c}{\displaystyle R\beta =a-A}\end{array}$ (11) egyenletek teljesülnek. Az (1)‐(6), (10), (11) egyenletrendszert megoldva a következő eredményeket kapjuk: $\begin{array}{c}{\displaystyle a=\frac{7}{2}\frac{F-\mu \left(m+M\right)g}{M+\frac{7}{2}m}\mathrm{,}A=\frac{F-\mu \left(m+M\right)g}{M+\frac{7}{2}m}\mathrm{,}\beta =\frac{5}{2R}\frac{F-\mu \left(m+M\right)g}{M+\frac{7}{2}m}\mathrm{.}}\end{array}$ Szükségünk van még a golyó szögsebességére hosszú idő elteltével, azaz jóval a fólia kihúzása után. Ehhez először számítsuk ki, hogy mennyi ideig marad a fólián a golyó. A golyó gyorsulása a fóliához képest $a-A$, így a leesésig eltelt $t_1$ időre igaz a következő: 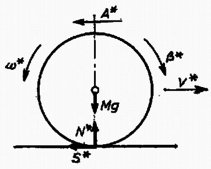$\begin{array}{c}{\displaystyle l=\left(1/2\right)\left(a-A\right)t_1^2\mathrm{,}}\end{array}$ ahonnan $\begin{array}{c}{\displaystyle t_1=\sqrt[]{\frac{2l}{a-A}}\mathrm{.}}\end{array}$ Így a golyó szögsebessége a leesés pillanatában $\begin{array}{c}{\displaystyle {\omega }_1=\beta t_1=\sqrt[]{\frac{2l\beta }{R}}\mathrm{.}}\end{array}$ A golyó sebessége ekkor $\begin{array}{c}{\displaystyle v_1=A{t}_1=\left(2/5\right)\sqrt[]{2lR\beta }\mathrm{.}}\end{array}$     3. ábra Nagyon lényeges körülmény azonban az, hogy a golyó a sebességének megfelelő forgásiránnyal ellentétes irányban forog. A golyó mozgásegyenletei a talajra érkezés után (3. ábra): ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle M{A}^{*}}& {\displaystyle =S^{*}\mathrm{,}}\hfill & \text{(<mrow><msup><mrow><mn>1</mn></mrow><mrow><mo>*</mo></mrow></msup></mrow>)}\\ \hfill {\displaystyle 0}& {\displaystyle =Mg-N^{*}\mathrm{,}}\hfill & \text{(<mrow><msup><mrow><mn>2</mn></mrow><mrow><mo>*</mo></mrow></msup></mrow>)}\\ \hfill {\displaystyle \Theta {\beta }^{*}}& {\displaystyle =S^{*}R;}\hfill & \text{(<mrow><msup><mrow><mn>3</mn></mrow><mrow><mo>*</mo></mrow></msup></mrow>)}\end{array}}$ valamint amíg a köszörülés (csúszva gurulás) tart, addig ${\displaystyle \begin{array}{cc}\hfill {\displaystyle S^{*}=\mu N^{*}\mathrm{.}}& \text{(<mrow><msup><mrow><mn>4</mn></mrow><mrow><mi>*</mi></mrow></msup></mrow>)}\end{array}}$ Az (1${}^{*}$)‐(4${}^{*}$), (6) egyenletrendszert megoldva kapjuk, hogy $\begin{array}{c}{\displaystyle A^{*}=\mu g\mathrm{,}{\beta }^{*}=\left(5/2\right)\mu g/R\mathrm{.}}\end{array}$ Így a golyó sebessége $\begin{array}{c}{\displaystyle v^{*}=v_1-A^{*}t\mathrm{,}}\end{array}$ szögsebessége pedig $\begin{array}{c}{\displaystyle {\omega }^{*}={\omega }_1-{\beta }^{*}t}\end{array}$ alakban függ az időtől. A köszörülés abban a $t_2$ időpillanatban fejeződik be, amikor a golyó sebessége és szögsebessége kielégíti a gördülés $\begin{array}{c}{\displaystyle v^{*}=-{\omega }^{*}R}\end{array}$ feltételét. Behelyettesítés után kapjuk, hogy $\begin{array}{c}{\displaystyle t_2=\frac{2}{7}\frac{v_1+\omega R}{\mu g}=\frac{2}{5}\frac{\sqrt[]{2lR\beta }}{\mu g}\mathrm{.}}\end{array}$ A keresett $\omega$ értéket az ${\omega }^{*}$ adja meg, ha behelyettesítjük a $t_2$ időt: $\begin{array}{c}{\displaystyle \omega ={\omega }^{*}\left(t_2\right)={\omega }_1-{\beta }^{*}{t}_2=0.}\end{array}$ Így ‐ érdekes módon ‐ a golyó, miután elhagyta a fóliát, $t_2$ idő múlva megáll. A b) eset megvalósulásának az a feltétele, hogy ne következzék be csúszás a golyó és a fólia között, azaz $\begin{array}{c}{\displaystyle S\le \mu N\mathrm{,}}\end{array}$ (12) vagyis ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A}& {\displaystyle \le \mu g\mathrm{,}}\hfill \\ \hfill {\displaystyle F}& {\displaystyle \le \mu g\left[2M+\left(9/2\right)m\right]}\hfill \end{array}}$ legyen.   c) Ha $\begin{array}{c}{\displaystyle F>\mu g\left[2M+\left(9/2\right)m\right]\mathrm{,}}\end{array}$ akkor az (1)‐(6), (10) egyenletekhez az $\begin{array}{c}{\displaystyle S=\mu N}\end{array}$ (13) egyenlet csatlakozik, mivel a golyó és a fólia egymáson csúsznak. Az egyenletrendszert megoldva kapjuk, hogy $\begin{array}{c}{\displaystyle a=\frac{F-\mu g\left(2M+m\right)}{m}\mathrm{,}A=\mu g\mathrm{,}\beta =\frac{5}{2}\frac{\mu g}{R}\mathrm{.}}\end{array}$ Ebben az esetben ismét ki kell számítanunk a golyó szögsebességét a talajra érést követő köszörülés befejezése után. A b) esethez hasonlóan a leesésig eltelt idő $\begin{array}{c}{\displaystyle t_3=\sqrt[]{\frac{2l}{a-A}}\mathrm{.}}\end{array}$ A golyó szögsebessége a leesés pillanatában $\begin{array}{c}{\displaystyle {\omega }_3=\beta t_3=\frac{5}{2}\frac{\mu g}{R}\sqrt[]{\frac{2lm}{F-2\mu g\left(M+m\right)}}\mathrm{.}}\end{array}$ A golyó sebessége ekkor $\begin{array}{c}{\displaystyle v_3=A{t}_3=\mu g\sqrt[]{\frac{2lm}{F-2\mu g\left(M+m\right)}}\mathrm{.}}\end{array}$ Természetes, hogy az (1${}^{*}$)‐(4${}^{*}$), (6) egyenletrendszer írja le most is a mozgást, azaz az előző pontban felírt ${\beta }^{*}$ és $A^{*}$ értékekkel számolhatunk. A golyó sebessége a köszörülés során $\begin{array}{c}{\displaystyle v^{*}=v_3-A^{*}t\mathrm{,}}\end{array}$ szögsebessége $\begin{array}{c}{\displaystyle {\omega }^{*}={\omega }_3-{\beta }^{*}t\mathrm{.}}\end{array}$ A $\begin{array}{c}{\displaystyle v^{*}=-{\omega }^{*}R}\end{array}$ egyenletből kifejezve a köszörülés időtartamát, azt kapjuk, hogy a köszörülés befejezésének időpontja $\begin{array}{c}{\displaystyle t_4=\frac{2}{7}\frac{v_3+{\omega }_{3}R}{\mu g}=\sqrt[]{\frac{2lm}{F-2\mu g\left(m+M\right)}}\mathrm{.}}\end{array}$ A keresett $\omega$ értéket az ${\omega }^{*}\left(t_4\right)$ behelyettesítéssel számíthatjuk ki: $\begin{array}{c}{\displaystyle \omega ={\omega }^{*}\left(t_4\right)={\omega }_3-{\beta }^{*}t=0.}\end{array}$ Ismét azt kaptuk, hogy a golyó állva marad. A numerikus adatok felhasználásával nyert eredményeinket a 4. ábrán szemléltetjük. 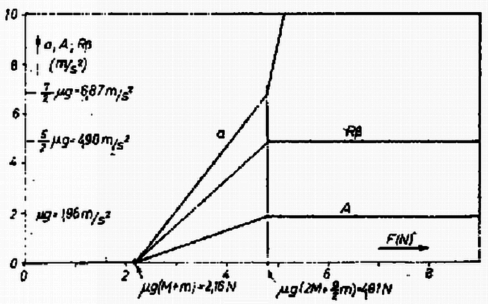    4. ábra  Csók Tibor (Kecskemét, Katona J. Gimn., IV. o. t.)  dolgozata alapján   Megjegyzés. Az impulzus és impulzusmomentum tételének alkalmazásával közvetlenül és egyszerűen bizonyítható, hogy a golyó a végén állva marad.