Feladat:	1469. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Jancsó Péter
Füzet:	1978/szeptember, 39 - 41. oldal		PDF  |  MathML
Témakör(ök):	Energiamegmaradás tétele, Hajítások, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1977/december: 1469. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.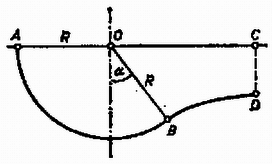   Tekintsük a légtornászt pontszerűnek! A légtornász lengésekor a helyzeti és mozgási energia összege állandó, így a légtornász a $h=R\text{cos}\alpha$ magasból történő esés sebességével hagyja el a hintát a $B$ pontban (1. ábra): 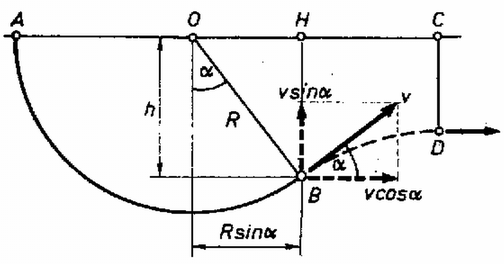$\begin{array}{c}{\displaystyle v=\sqrt[]{2gR\text{cos}\alpha }\mathrm{.}}\end{array}$ (1) A légtornász tömegközéppontja a továbbiakban ekkora kezdősebességű ferde hajítási pályán mozog. A kezdősebesség $\alpha$ szöget zár be a vízszintessel, így $B$-ben a sebesség függőleges és vízszintes összetevője $v\text{sin}\alpha$, ill. $v\text{cos}\alpha$.     1. ábra   Jelöljük $t$-vel a $B$ és $D$ pont közötti repülés idejét! Mivel $D$ a pálya tetőpontja, a függőleges sebességösszetevő itt nullává válik: $\begin{array}{c}{\displaystyle v\text{sin}\alpha -gt=0.}\end{array}$ (2) Ugyanennyi idő alatt a vízszintes elmozdulás: $\begin{array}{c}{\displaystyle t\cdot v\text{cos}\alpha =\overline{HC}=\overline{OC}-R\text{sin}\alpha \mathrm{.}}\end{array}$ (3) Az (1), (2), (3) egyenletekből $\text{sin}\alpha$-ra kapjuk: $\begin{array}{c}{\displaystyle 3\text{sin}\alpha -2\text{sin}{}^3\alpha -\overline{OC}/R=0.}\end{array}$ Numerikusan ($\overline{OC}=\mathrm{13,7}$ m, $R=10$ m): $\begin{array}{c}{\displaystyle 3\text{sin}\alpha -2\text{sin}{}^3\alpha -\mathrm{13,7}=0.}\end{array}$ Ennek a harmadfokú egyenletnek a megoldásához néhány pontban kiszámítottuk és a következő táblázatban megadtuk az 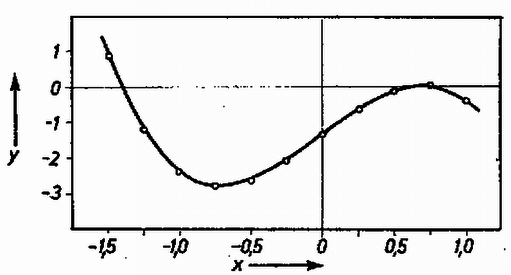$\begin{array}{c}{\displaystyle y=3x-2x^3-\mathrm{13,7}}\end{array}$ függvény értékeit:   ${\displaystyle \begin{array}{cccccccccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,7</mn></math>5}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,5</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,25</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,25</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,5</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,75</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1,25</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1,5</mn></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,370</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,036</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,120</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,651</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1,370</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2,089</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2,620</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2,776</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>2370</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1,214</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0,880</mn></math>}}\hfill \end{array}}$     2. ábra   Az ezekből az adatokból rajzolt 2. ábrán láthatjuk, hogy a függvény három nullhelye közül a legkisebb 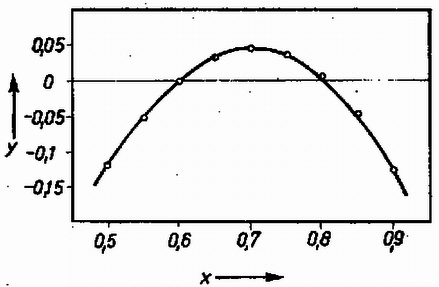$\left(-\mathrm{1,4}\right)$ nem lehet szinusz érték, a másik két gyök pontosabb meghatározásához pedig még célszerű újabb behelyettesítéseket végezni: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cccccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,55</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,6</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,65</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,7</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,8</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,85</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,9</mn></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,053</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,0002</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,031</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,044</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,006</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>1,048</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,128</mn></math>}}\hfill \end{array}}}\end{array}$     3. ábra   A 3. ábráról már egészen pontosan leolvashatjuk a gyököket. Még két pontban érdemes behelyettesíteni a függvénybe, és a következő táblázatból már lineáris interpolációval kapjuk a megfelelően pontos gyököket: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{ccccc}\hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>x</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,60</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,61</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,80</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,81</mn></math>}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,0020</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0,0060</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mn>1</mn><mspace width="0.3mm"></mspace></mphantom><mn>0,0060</mn></math>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mo stretchy="false">-</mo><mn>0,0029</mn></math>}}\hfill \end{array}}}\end{array}$ Innen a harmadfokú függvény nullhelyei $\begin{array}{c}{\displaystyle x_1=\mathrm{0,603,}{x}_2=\mathrm{0,807.}}\end{array}$ A feladat megoldásai tehát az $\begin{array}{c}{\displaystyle {\alpha }_1={37}^{\circ }5\text{'};{\alpha }_2={53}^{\circ }50\text{'}}\end{array}$ szögek. A hajítás maximális emelkedése (1) és (2) alapján $\begin{array}{c}{\displaystyle h=t\cdot v\text{sin}\alpha -\frac{g}{2}{t}^2=\frac{v^2\text{sin}{}^2\alpha }{2g}=}\end{array}$ $\begin{array}{c}{\displaystyle =R\cdot \text{cos}\alpha \cdot \text{sin}{}^2\alpha \mathrm{.}}\end{array}$ Így $\begin{array}{c}{\displaystyle \overline{CD}=R\text{cos}\alpha -h=R\text{cos}{}^3\alpha \mathrm{.}}\end{array}$ Az ${\alpha }_1$, ill. ${\alpha }_2$ megoldás felhasználásával $\begin{array}{c}{\displaystyle {\left(\overline{CD}\right)}_1=\mathrm{5,08}\text{m};{\left(\overline{CD}\right)}_2=\mathrm{2,05}\text{m}\mathrm{.}}\end{array}$ A $B$ és $D$ közötti repülési idő (2)-ből: $\begin{array}{c}{\displaystyle t=\frac{v\text{sin}\alpha }{g}=\frac{\sqrt[]{2Rg\text{cos}\alpha }\cdot \text{sin}\alpha }{g}\mathrm{.}}\end{array}$ Numerikusan: $\begin{array}{c}{\displaystyle t_1=\mathrm{0,77}\text{s}\mathrm{,}{t}_2=\mathrm{0,88}\text{s}\mathrm{.}}\end{array}$    Jancsó Péter (Sopron, Széchenyi I. Gimn., III. o. t.)  dolgozata alapján