Feladat:	1457. fizika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Csikós Balázs ,  Farkas Ferenc ,  János Mihály ,  Kálvin Sándor ,  Kaufmann Zoltán ,  Litvai Ibolya ,  Mészáros Gyula ,  Oszvald Elemér ,  Sas Viktor ,  Udvardi László ,  Varga Tamás Péter
Füzet:	1978/március, 138 - 139. oldal		PDF  |  MathML
Témakör(ök):	Feszültségmérés (voltmérő), Ellenállások kapcsolása, Egyéb Ohm-törvény, Feladat
Hivatkozás(ok):	Feladatok: 1977/október: 1457. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     A kimenő feszültség, mint a csúszka helyzetének függvénye, közelítőleg szimmetrikus a csúszka középső helyzetére vonatkozólag, továbbá sima függvény. Ezért szükségünk van egy olyan kapcsolási elemre, amelynek ellenállása a csúszka két különböző helyzetében azonos. Ilyen kapcsolás látható az 1. ábrán, eredő ellenállása: $\begin{array}{c}{\displaystyle R_e=\frac{x\left(R-x\right)}{R}\mathrm{.}}\end{array}$ (1)     1. ábra     2. 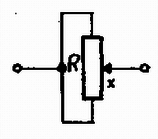ábra   Ha ezt az elrendezést egy Wheatstone-híd egyik ellenállásának helyére építjük be, az ellenállások megfelelő megválasztásával feszültség kívánt változása megvalósítható (2. ábra). Mivel a kimenő feszültség a csúszka két szélső helyzetében nem pontosan azonos, a potenciométer mellé egy kis $R_4$ ellenállást is kell kapcsolnunk. A telep feszültségének $5$ V-nál nagyobbnak kell lennie. Hogy a kapcsolás fogyasztása ne legyen szükségtelenül nagy, legyen $\begin{array}{c}{\displaystyle U=6\text{ V}\mathrm{.}}\end{array}$ A csúszka alsó helyzetében a kimenő feszültség az $R_2$ ellenálláson eső feszültséggel egyezik meg. $R_2$-n akkor esik $2$ V, ha $R_1:R_2=4\text{ V}:2\text{ V}$. Az ellenállások abszolút értéke szabadon választható. Célszerű minél nagyobb ellenállásokat használni, hogy a hálózat fogyasztása ne legyen túlságosan nagy. Ugyanakkor jóval kisebb ellenállásokat kell használnunk, mint a hálózatot terhelő kapcsolás bemenő ellenállása, ellenkező esetben a kimenő feszültséget a terhelés lényegesen megváltoztatja. Tegyük fel, hogy a hálózathoz egy $10\text{ k}\Omega$ bemenő ellenállású tranzisztoros erősítő kapcsolódik, és néhány százalékos pontossággal megelégszünk. Így lehet pl. $\begin{array}{c}{\displaystyle R_1=200\Omega \mathrm{,}{R}_2=100\Omega \mathrm{.}}\end{array}$ A potenciométer csúszkája ekkor a földhöz képest $-2$ V feszültségen van. A csúszka másik szélső helyzetében az $R_3$ ellenálláson $5$ V feszültség esik, így $\begin{array}{c}{\displaystyle 6\text{ V}\cdot \frac{R_3}{R_3+\frac{R{R}_4}{R+R_4}}=5\text{ V}\mathrm{.}}\end{array}$ (2) A kimenő feszültség akkor a legnagyobb, amikor a 2. ábra kapcsolásának ellenállása maximális, vagyis amikor a csúszka felezi az $R_4+R$ ellenállást. Ekkor az $R_2$ ellenálláson $1$ V feszültség esik, $\begin{array}{c}{\displaystyle 6\text{ V}\cdot \frac{R_3}{R_3+\frac{R+R_4}{4}}=1\text{ V}\mathrm{.}}\end{array}$ (3) Egy ellenállást ismét szabadon választhatunk, legyen pl. $\begin{array}{c}{\displaystyle R_3=10\Omega \mathrm{.}}\end{array}$ Ekkor (2)-ből és (3)-ból $\begin{array}{c}{\displaystyle R=198\Omega \mathrm{,}{R}_4=2\Omega \mathrm{.}}\end{array}$    Varga Tamás Péter (Tata, Eötvös J. Gimn., IV. o. t.)  dolgozata alapján