|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.
I. megoldás. A Fermat‐elv szerint a fény két pont között mindig azon az úton halad, amelynek megtételéhez a legrövidebb idő szükséges. Az pontról így csak akkor keletkezhet egy pontban valódi kép, ha az -ból különböző irányokban kiinduló fénysugarak ugyanannyi idő alatt érnek -be, vagyis -ben ismét összegyűlnek (1. ábra). Hasonlítsuk össze az optikai tengelyen és egy attól különböző, vele kis szöget bezáró irányban haladó fénysugárnak az és pont közötti út megtételéhez szükséges idejét ( a fény sebessége vákuumban): | |
azaz
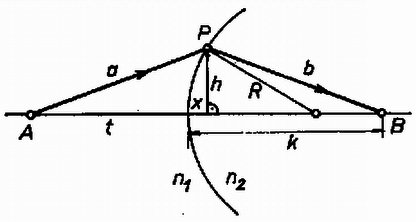 1. ábra
Fejezzük ki -t és -t -vel, -val és -val! Ehhez szükségünk lesz az távolság ismeretére: | | (2) |
Itt felhasználtuk, hogy , tehát érvényes a közelítés. Felhasználva, hogy : | |
értékét (2)-ből beírva és hasonlóan (3)-at és (4)-et behelyettesítve (1)-be és rendezve, a rendszer leképezési törvényét kapjuk az optikai tengellyel kis szöget bezáró fénysugarak esetén: | | (5) |
(A leképezési törvényt valódi kép esetére vezettük le. Belátható, hogy a szokásos előjel konvenció szerint látszólagos kép esetén is alkalmazható.)
(5)-ből a képtávolság Valódi kép akkor keletkezik, ha (6) nevezője pozitív,
A felület két oldalán különböző a fókusztávolság. A bal oldali fókusztávolságot úgy kapjuk meg, hogy (6) felhasználásával megnézzük: esetén mi határértéke (a fókuszból induló sugarak a határfelületen túl párhuzamosan haladnak), így nyerjük: A párhuzamosan érkező fénysugarak a jobb oldali fókuszpontban gyűlnek össze. (6) alapján esetén határértéke: A (7) feltételek így azt fejezik ki, hogy akkor keletkezik valódi kép, ha a fókusztávolság pozitív (gyűjtőlencse) és a tárgy a fókusztávolságon kívül van.
Tóth Csaba (Sopron, Széchenyi I. Gimn., IV. o. t.)
II. megoldás. A leképezési törvényt a fénytörés törvényét felhasználva is megkaphatjuk. A 2. ábra alapján Kis szögek esetén a szög ívmértékben vett értéke, sinusa és tangense megegyezik, így
ahol
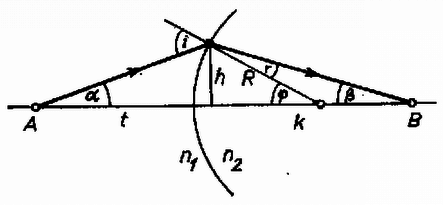 2. ábra
Ezeket az összefüggéseket (2)-be beírva és rendezve az | | (3) |
leképezési törvényt kapjuk.
Benkő Zsigmond (Szolnok, Verseghy F. Gimn., II. o. t.) |
|
 PDF |
PDF |  MathML
MathML 
