Kezdőlap


Feladat:	1431. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Benkő Zsigmond , Czuczor Lajos , Frey István , Katona Gábor , Kriza György , Németh Gábor
Füzet:	1977/december, 231 - 233. oldal		PDF \| MathML
Témakör(ök):	Merev testek ütközése, Tehetetlenségi nyomaték, Energiamegmaradás, Impulzusnyomaték (perdület) megmaradása, Határozott integrál, Feladat
Hivatkozás(ok):	Feladatok: 1977/április: 1431. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tételezzük fel, hogy az ütközés időtartama az inga lengésidejéhez képest elhanyagolhatóan kicsiny. Közvetlenül az ütközés után az ingát ezért még függőlegesnek tekinthetjük, így az ingából és a lövedékből álló rendszerre ható külső erők hatásvonala átmegy a $P$ felfüggesztési ponton. Erre a pontra vonatkoztatva tehát a rendszerre külső forgatónyomaték nem hat, azaz az ütközés folyamán impulzusmomentuma nem változik. Az ütközés előtti impulzusmomentum:

\begin{matrix} N_{1} = m v l, \end{matrix}

(1)

közvetlenül az ütközés után:

\begin{matrix} N_{1} = Θ ω \end{matrix}

(2)

ahol

ω

az inga szögsebessége,

Θ

a rendszernek a

P

pontra vonatkozó tehetetlenségi nyomatéka az ütközés után:

\begin{matrix} Θ = m l^{2} + M_{1} l^{2} + (1 / 3) M l^{2} . \end{matrix}

(3)

Feltettük, hogy a lövedék a

M_{1}

-et tartó csuklóhoz közel állt meg, így a

P

ponttól való távolsága

l

-nek tekinthető. Az impulzusmomentum nem változott:

\begin{matrix} N_{1} = N_{2} . \end{matrix}

(1) és (2) felhasználásával az

\begin{matrix} ω = \frac{m v l}{Θ} \end{matrix}

(4)

egyenlőséghez jutunk.
Következő lépésként a munkatételt alkalmazzuk. A rendszeren a nehézségi erő által végzett munka megegyezik a rendszer mozgási energiájának megváltozásával. Jelöljük a maximális kitérés szögét

φ_{0}

-lal ‐ itt az inga nyugalomban van ‐ az inga mozgási energiáját

φ

szögű helyzetében

E (φ)

-vel!

Ekkor a mozgási energia megváltozása:

\begin{matrix} E (φ_{0}) - E (0) = - (1 / 2) Θ ω^{2} . \end{matrix}

(5)

(Feltevésünk szerint a

m

tömegű lövedék a csuklóhoz közel állt meg. A

M_{1}

és

m

tömegű testekből álló fizikai inga lengésideje ezért igen nagy. Így

M_{1}

elfordulása a maximális kitéréskor még elhanyagolható, saját forgási energiával nem rendelkezik.)
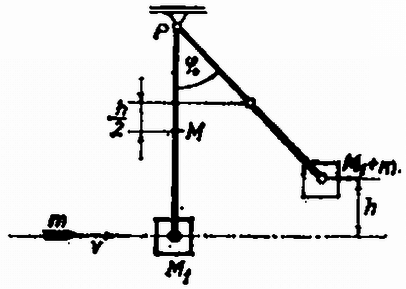
Figyelembe véve, hogy a lövedék és a

M_{1}

tömeg súlypontja a maximális kitéréskor még közel egy magasságban van, és a nehézségi erő ellenében történik a munkavégzés, a nehézségi erő munkája (l. az ábrát):

\begin{matrix} W = - (M_{1} + m) g h - M g (h / 2) = - g [M_{1} + m + (1 / 2) M] l (1 - cos φ_{0}) . \end{matrix}

(6)

A munkatétel szerint:

\begin{matrix} W = E (φ_{0}) - E (0) . \end{matrix}

(5) és (6) alapján a következő egyenlőséghez jutunk:

\begin{matrix} - (1 / 2) Θ ω^{2} = - g l (1 - cos φ_{0} [M_{1} + m + (M / 2)] . \end{matrix}

Ebből (3) és (4) felhasználásával a maximális kitérésnél

\begin{matrix} cos φ_{0} = l - \frac{m^{2} v^{2}}{g l [M_{1} + m + (1 / 3) M] (2 M_{1} + 2 m + M)} . \end{matrix}

Ha ebből a képletből

cos φ < - 1

adódik, maximális kitérésről nem beszélhetünk; ekkor az inga körbefordul.

Benkő Zsigmond (Szolnok, Verseghy F. Gimn., II. o. t.)

Megjegyzés. Az inga közvetlenül ütközés utáni szögsebességét másképp is kiszámíthatjuk. Newton II. törvénye szerint a lövedék lassítását okozó erő időintegrálja megegyezik az ütközés utáni és előtti impulzusok különbségével. Ha

τ

az ütközés ideje,

ω

az ütközés utáni szögsebesség és

I (t)

t

időpontbeli impulzus, akkor:

\begin{matrix} \int_{0}^{τ} F d t = I (τ) - I (0) = m ω l - m v . \end{matrix}

(7)

Az ingára ható forgatónyomaték idő szerinti integrálja megegyezik az ütközés utáni és előtti impulzusmomentumok különbségével. Newton III. törvénye szerint a lövedéket lassító

F

erő ellenerejének a forgatónyomatéka hat az ingára. Ha

τ

igen kicsi,

F

erőkarja

l

-nek vehető:

\begin{matrix} \int_{0}^{τ} (- F l) d l = N (τ) - N (0) = [M_{1} + (1 / 3) M] l^{2} ω . \end{matrix}

(8)

A (7) és (8) egyenletek összevetéséből

ω

-ra (4)-gyel megegyező kifejezést kapunk.

Czuczor Lajos (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)